EXTRA DE VERANO (1 DE JULIO DE
Problema 259
8. Sobre los lados de un triángulo ABC se dan pares de
puntos A1-A2, B1-B2, C1-C2, tales que
A1B/A1C=A2C/A2B=B1C/B1A=B2A/B2C=C1A/C1B=C2B/C2A=m.
Hallar la razón de áreas entre el triángulo dado y el que
tiene por vértices los puntos A´=BB1 intersección
CC2, B´= CC1
intersección con AA2, C´= AA1 intersección BB2-
Matemática Elemental, (1941): N.2, páginas 69-70,
SoluciónMaite Peña Alcaraz, estudiante de Industriales en la
Universidad de Comillas (Madrid) :
Tomemos el
triángulo colocado sobre unos ejes de la siguiente forma:
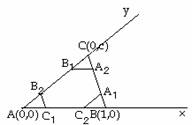Con
estos ejes las coordenadas de los puntos
serían fáciles de calcular:
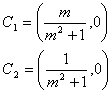
Así que las rectas quedan como:
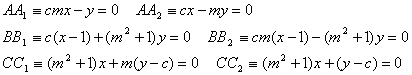
Y los puntos A’, B’ y C’ del triángulo
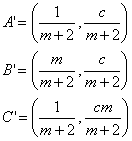
y por tanto A’ y B’ distan 
frente a AB que distan
1 y la razón entre las áreas es por tanto 
.