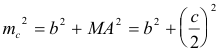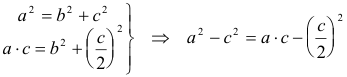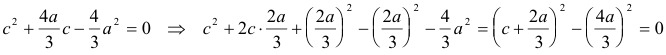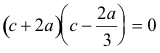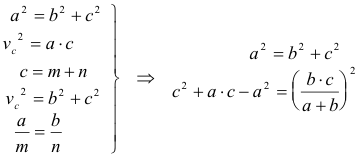Problema 260 Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid Caracterizar y construir los triángulos rectángulos de catetos c y b con c<b, y a, de hipotenusa tales que ; a) la mediana mc es la medía geométrica de a y c; b) la bisectriz vc, es la media geométrica de a y c.
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (7 de julio de 2005) |
|
CARACTERIZACIÓN DE LOS TRIÁNGULOS |
|
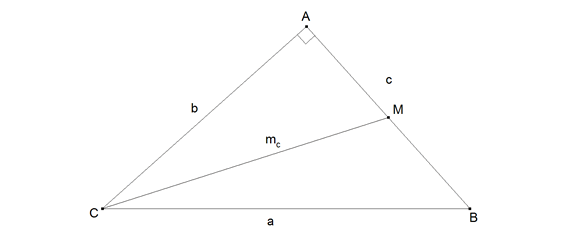
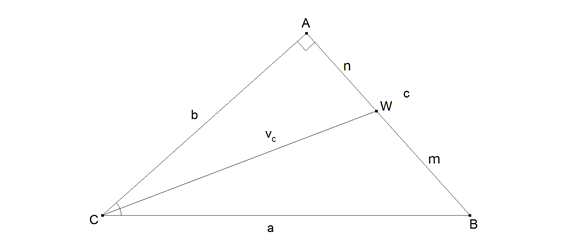
CASO (a) Si suponemos el problema resuelto en la figura 1 deducimos las ecuaciones que caracterizan al problema
figura 1
Por ser triángulo rectángulo:
Por ser media geométrica
Por ser mediana
Y nos queda
c es la solución positiva de
y obtenemos
LA CARACTERIZACIÓN DEL TRIÁNGULO RECTÁNGULO ES QUE SU CATETO MENOR ES IGUAL A LAS DOS TERCERAS PARTES DE LA HIPOTENUSA
que permite una fácil construcción.
|
|
CASO (b)
figura 2 Por ser triángulo rectángulo:
Por ser media geométrica
Teniendo en cuenta el pie de la bisectriz
Por ser bisectriz
Y por el teorema de la bisectriz
Para obtener c en función de a, llegaríamos a la solución de un polinomio de quinto grado en c. Este polinomio no es trivial. Si eliminamos vc, m y n obtenemos la caracterización de estos triángulos por medio de dos ecuaciones que nos ligan los catetos con la hipotenusa
|
|
PASO PREVIO A LA CONSTRUCCIÓN |
|
LA MEDIA GEOMÉTRICA - POTENCIA DE UN PUNTO RESPECTO A UN CIRCULO El caso (a) y el caso (b) tienen una construcción en común; el trazado de la media geométrica.
figura 3 Determinada la potencia de un punto C respecto a un círculo, vemos que la tangente del punto al círculo es la media geométrica de los dos segmentos que se forman en la recta que une al punto con el centro del círculo.
|
|
LA MEDIA GEOMÉTRICAS DE HIPOTENUSA Y CATETO EN UN TRIÁNGULO RECTÁNGULO
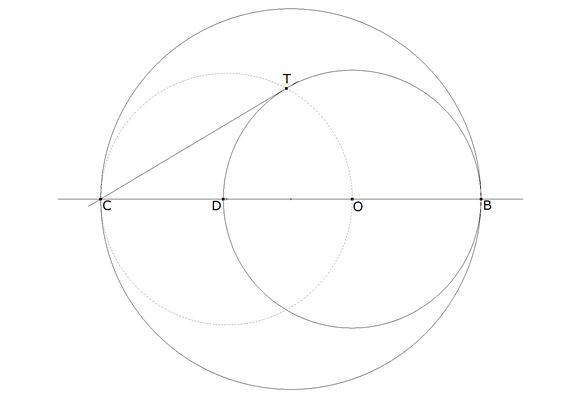
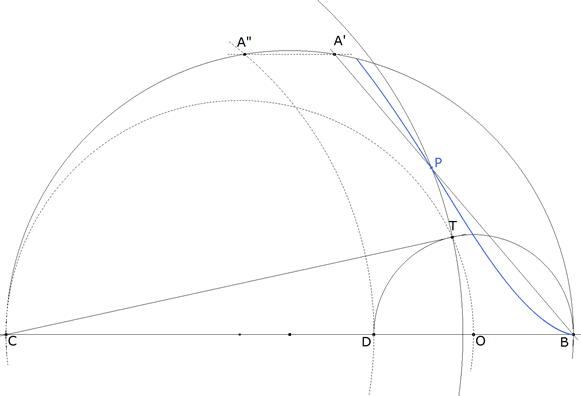
figura 4 Sea el círculo de diámetro BC=a (hipotenusa del triángulo buscado). Sobre dicho círculo tomamos A’ vértice de un triángulo rectángulo cualquiera.. Por A’ trazamos una paralela a BC que corta al círculo en A”. Por simetría BA’=CA”. Con centro en C, círculo de radio CA” que corta a BC en D. Trazamos el círculo de diámetro DB al que trazamos la tangente CT desde C. Recordando el párrafo anterior:
CT ES LA MEDIA GEOMÉTRICA DE LA HIPOTENUSA a Y EL CATETO c
|
|
LUGAR GEOMÉTRICO DE LAS MEDIAS GEOMÉTRICAS DE HIPOTENUSA Y CATETO
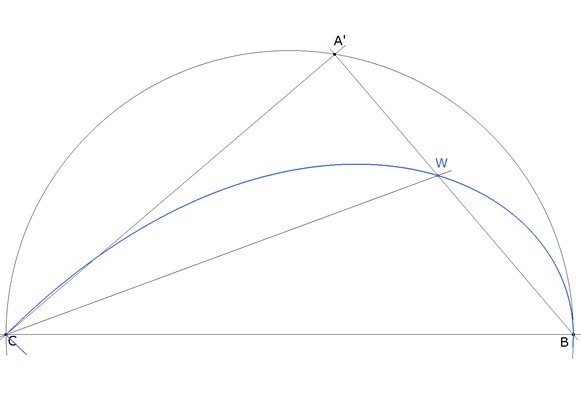
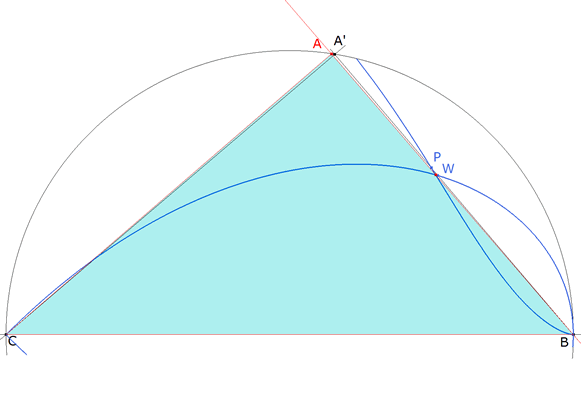
figura 5 Sabemos que CT es igual a la media geométrica de hipotenusa y cateto. El círculo de centro C y radio CT corta al cateto A’B en P y por tanto P es el punto sobre el cateto cuya distancia al vértice opuesto es la media geométrica del cateto y la hipotenusa. Si desplazamos A’ sobre su círculo obtenemos (en azul - figura 5) el lugar geométrico de los puntos sobre el cateto cuya distancia al vértice opuesto es la media geométrica del cateto y la hipotenusa.
|
|
LA CONSTRUCCIÓN |
|
CASO (a) - LUGAR GEOMÉTRICO DEL PUNTO MEDIO DEL CATETO. Ya hemos visto en la caracterización del triángulo que para la construcción nos basta tomar el cateto igual a los dos tercios de la hipotenusa: pero nosotros usaremos otro método basado en lugares geométricos, que se aplicará perfectamente también en el caso (b).
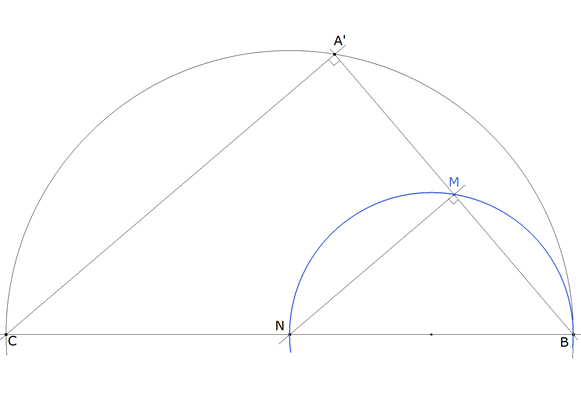
figura 6 Considerando el mismo triángulo A’BC del apartado anterior y siendo M el punto medio del cateto A’B; el lugar geométrico de M al desplazar A’ sobre el círculo es otro círculo homotético al original con centro de homotecia en B y razón ½.
|
|
CASO (a) FINAL
figura 7
|
|
CASO (b) - LUGAR GEOMÉTRICO DEL PIE DE LA BISECTRIZ SOBRE EL CATETO.
figura 8
|
|
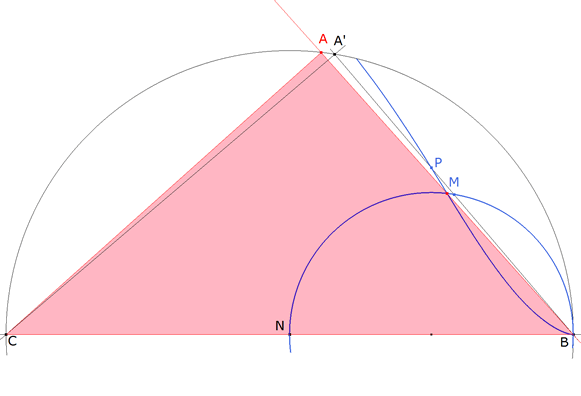
CASO (b) FINAL EL PUNTO BUSCADO DEBE SER A LA VEZ PIE DE BISECTRIZ SOBRE EL CATETO Y MEDIA GEOMÉTRICA DE HIPOTENUSA Y CATETO; POR LO TANTO LA SOLUCIÓN SE ENCONTRARÁ EN LA INTERSECCIÓN DE LOS DOS LUGARES
figura 9
|