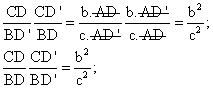Problema 261.-
Dado el triángulo ABC, Supongamos que
D, E, y F son puntos sobre los lados BC, AC, y AB, respectivamente, y tales que
AD, BE, y CF concurren en un punto. Construimos las reflexiones del rayo AD con
respecto a la bisectriz de <BAC que corta a BC en D´. Similarmente definimos
E´y F´.
Demostrar que AD´, BE´, y CF´ son concurrentes.
Baragar, A. (2002) A survey of Classical and Modern Geometries with
computer
activities,
Propuesto por Juan Bosco Romero Márquez, profesor colaborador de
Solución
de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba,
España.
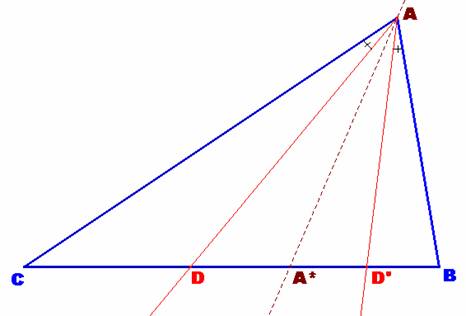
Examinamos, en primer lugar, una propiedad que nos va a conducir de forma inmediata a la solución del problema dado. Dada la figura siguiente, donde AA* representa la bisectriz interior del ángulo A, construimos AD’, recta isogonal[1] a la ceviana AD dada. Veamos la relación que determinan dichas cevianas sobre el lado opuesto BC.
|
|
|
Considerando los
triángulos ACD y ABD’, tendremos que su razón de áreas será igual a: Considerando ahora los
triángulos CAD’ y BAD, tendremos que su razón de áreas será igual a: Multiplicando ambas expresiones, obtenemos que:
|
Esta última relación es extensible al otro par de cevianas con sus respectivas isogonales.
Así, tendremos que:
|
|
|
Si multiplicamos las tres igualdades, resulta:
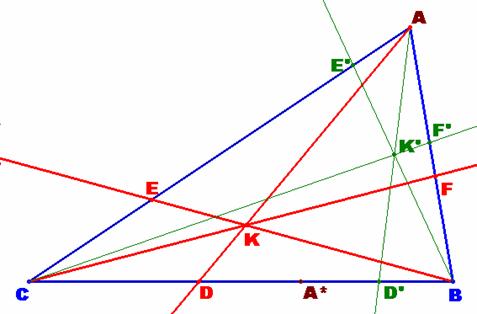
Ahora bien, Como por hipótesis, las
cevianas AD, BE y CF concurren en el punto K entonces, por el Teorema de Ceva
tendremos que Por tanto, |
;
; 
, lo que querrá decir, por el recíproco del Teorema de Ceva
que las cevianas AD’, BE’ y CF’ (isogonales de las cevianas AD, BE y CF)
concuren igualmente en un punto K’.