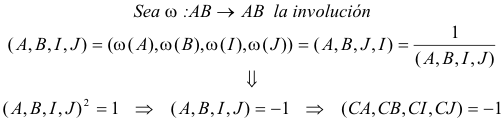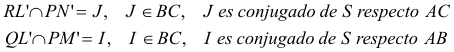Problema 261 Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid 1) Dado el triángulo ABC, Supongamos D, E, y F son puntos sobre los lados BC, AC, y AB, respectivamente, y tales que AD, BE, y CF concurren en un punto. Construimos las reflexiones del rayo AD con respecto a la bisectriz de <BAC que corta a BC en D́. Similarmente definimos Éy F́. Demostrar que AD́, BÉ, y CF́ son concurrentes.
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (12 de julio de 2005) |
|
INTRODUCCIÓN |
|
Vamos a resolver este problema empleando sólo GEOMETRÍA PROYECTIVA.
En particular, utilizamos las propiedades del CUADRIVÉRTICE (o de su dual el CUADRILÁTERO).
Aunque lo damos por conocido enunciaremos el TEOREMA DE CONCURRENCIA DE LAS BISECTRICES.
Enunciamos el TEOREMA DE PAPPUS y también el SEGUNDO TEOREMA DE DESARGUES que nos ayudan a mantener la solución en un plano más elemental. Estos teoremas se consideran conocidos y demostrados.
Demostramos las propiedades necesarias en el cuadrivértice o en el cuadrilátero. Y trasladamos los resultados de uno a otro por medio del PRINCIPIO DE DUALIDAD que también se considera conocido y demostrado.
|
|
DEFINICIONES |
|
EL CUADRIVÉRTICE (o cuadrángulo) Un cuadrivértice es la figura formada por cuatro puntos (tres a tres no alineados); cuatro puntos que reciben el nombre de vértices del cuadrivértice. Las rectas que unen los vértices dos a dos reciben el nombre de lados del cuadrivértice. Las intersecciones de los lados “opuestos” son los vértices diagonales. El triángulo formado por los tres vértices diagonales es el triángulo diagonal. El resultado fundamental concerniente a esta figura es el SEGUNDO TEOREMA DE DESARGUES. EL CUADRILÁTERO Un cuadrilátero es la figura formada por cuatro rectas (tres a tres no concurrentes); cuatro rectas que son los lados del cuadrilátero. Las intersecciones de esas cuatro rectas dos a dos son los vértices. Las rectas que unen dos vértices que no están sobre un mismo lado son las diagonales.
|
|
TEOREMAS SIN DEMOSTRACIÓN |
|
TEOREMA SOBRE LA CONCURRENCIA DE BISECTRICES Las bisectrices interiores de cualquier triángulo son concurrentes en un mismo punto. PRINCIPIO DE DUALIDAD A todo teorema de un espacio proyectivo, referente a propiedades de unión, intersección de subespacios del mismo, corresponde un teorema, llamado dual, de un espacio proyectivo el cual se obtiene cambiando en el enunciado primitivo
Y en el plano queda
Otro enunciado es:
“ Una proposición P relativa a subespacios de un espacio proyectivo es cierta si y sólo si lo es su proposición dual P*. “
TEOREMA DE PAPPUS
figura 1
figura 2
|
|
TEOREMAS CON DEMOSTRACIÓN |
|
TEOREMA UNO
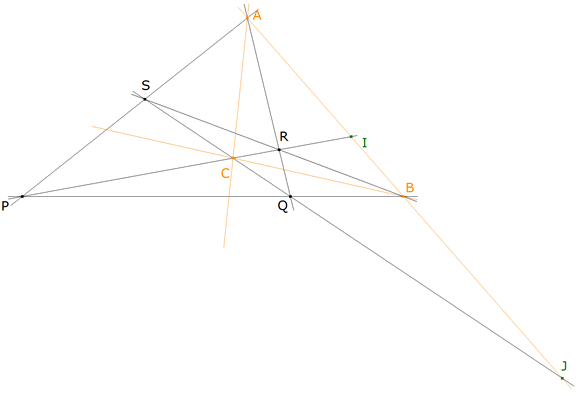
figura 3 DEMOSTRACIÓN UNO
Sean las rectas
Estas rectas cortan al lado AB en
Los puntos A y B son fijos en la involución que sobre AB se define según el SEGUNDO TEOREMA DE DESARGUES e I, J son homólogos en esta involución
|
|
TEOREMA DOS Si tres rectas l, m, n trazadas por los vértices diagonales de un cuadrivértice son concurrentes, sus rectas conjugadas l’, m’, n’ respecto a los lados del cuadrivértice también son concurrentes. DEMOSTRACIÓN DOS Daremos por demostrado este teorema, demostrando su dual (PRINCIPIO DE DUALIDAD): “ Si tres puntos L, M, N situados sobre las diagonales AA’, BB`, CC’ de un cuadrilátero están alineados sobre una recta d, los conjugados armónicos L’, M’, N’ respectivos de estos puntos respecto a los vértices están también alineados sobre una recta d’.”
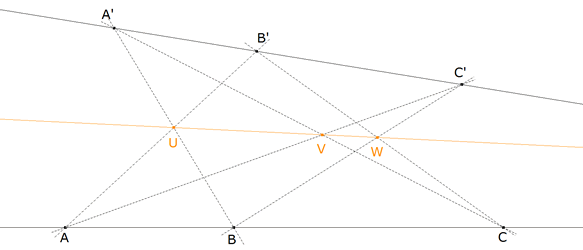
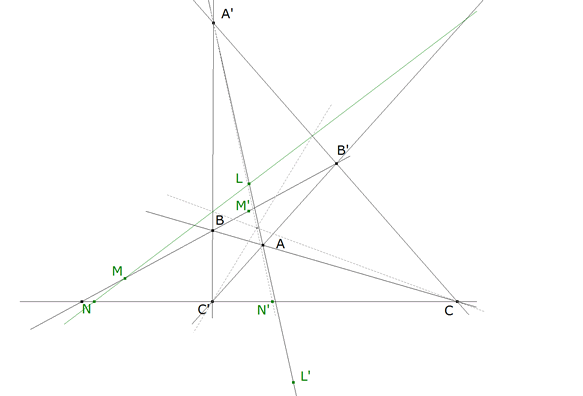
figura 4 Trazamos el cuadrilátero ABA’B’ de diagonales AA’, BB’, CC’. Trazamos la recta d (verde en la figura 4) y obtenemos L sobre AA’ M sobre BB’ N sobre CC’. Gracias al TEOREMA UNO sabemos trazar el conjugado armónico de un punto respecto a otros dos. En la figura 4 vemos el cálculo de N’ conjugado de N respecto CC’. Obtenemos: L’ conjugado armónico de L respecto AA’ M’ conjugado armónico de M respecto BB’ N’ conjugado armónico de N respecto CC’
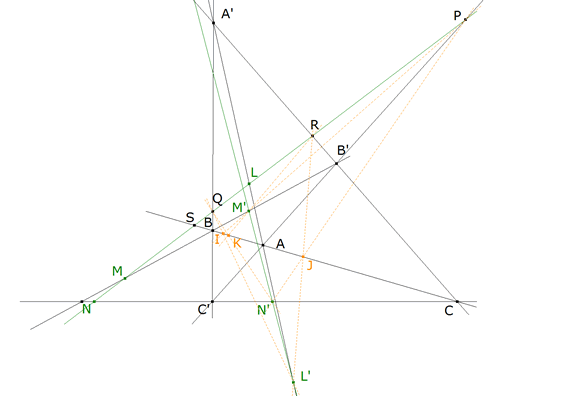
figura 5 La recta d corta a los lados del cuadrilátero en P, Q, R y S.
y de forma análoga
Pero el TEOREMA DE PAPPUS nos asegura que K’, M’, y N’ están alineados.
|
|
LA SOLUCION |
|
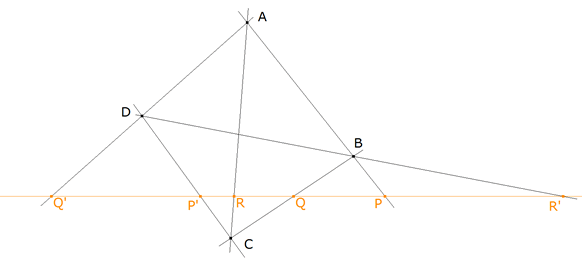
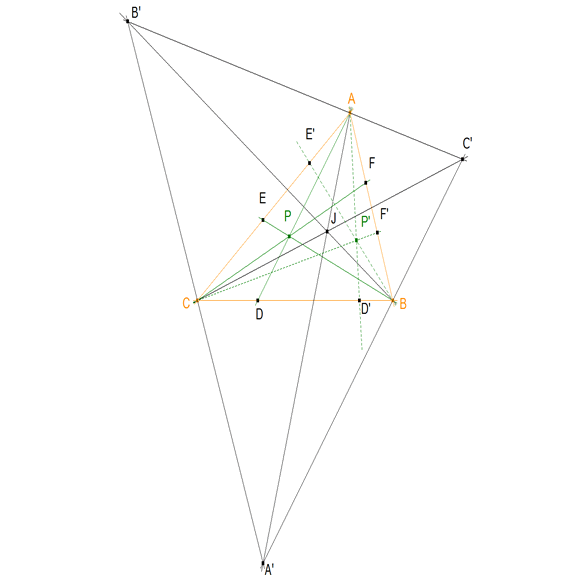
figura 6 Trazamos el enunciado. Sean A’, B’ C’ los vértices del triángulo formado por las bisectrices exteriores del triángulo ABC. Se sabe (TEOREMA CONCURRENCIA BISECTRICES) que las bisectrices interiores de un triángulo son concurrentes en un punto J; y de aquí, aunque no es la disposición típica, podemos ver que los puntos A’, B’, C’, J forman un cuadrivértice que tiene A, B, C como puntos diagonales. AB, BC, CA son las diagonales. Y ABC es el triángulo diagonal de este cuadrivértice. Por la simetría respecto a la bisectriz y por el TEOREMA UNO tenemos que: AD’ es el conjugado armónico de AD respecto a los lados que concurren en A, BE’ es el conjugado armónico de BE respecto a los lados que concurren en B, CF’ es el conjugado armónico de CF respecto a los lados que concurren en C,
LAS RECTAS AD’, BE’ Y CF’ SON CONCURRENTES EN UN PUNTO P’
|