Problema 262.-

Hallar todos los triángulos ABC con lados a, b y c que tiene la propiedad que la mediana desde A, la bisectriz en B, y la altura desde C, son concurrentes.

Guy (1995): My Favorite Elliptic Curve : A Tale of Two Types of Triangles.
The American Mathematical Monthly (Vol. 102, No. 9 (1995), pages 771-781.
Propuesto por Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid).

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba, España.

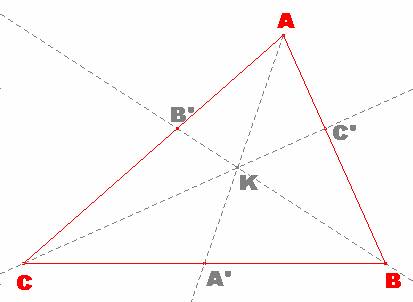
En el triángulo ABC dado con las condiciones exigidas, sean los siguientes segmentos:
AA’ = m_a (mediana); BB’= v_b (bisectriz); CC’= h_c (altura).
Si estas tres cevianas se cortan en un punto K, como se indica en el enunciado, tendremos que, según el Teorema de Ceva:

(I)

Teniendo en cuenta el teorema de la bisectriz, y que A’ es el punto medio del lado BC, entonces , entonces podemos expresar la identidad (I) como:
.
Si llamamos a los segmentos interceptados por la altura h_c en el lado AB, x e y, respectivamente, x = BC’ e y = C’A, entonces: .

Podemos resolver el sistema que nos proporciona las anteriores relaciones:
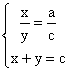, de donde obtenemos que:

Como quiera que BC’ ha de ser perpendicular con el segmento CC’, tenemos que A’, punto medio del lado BC será el centro de la circunferencia circunscrita del triángulo BCC’.

Estos dos últimos hechos nos proporcionan una herramienta valiosísima para poder construir el triángulo ABC. Veámoslo con mayor detalle.

Construcción a realizar:

1. Dados los lados BC=a y AB=c, cualesquiera, empezamos determinando el segmento . Para ello consideramos un trapecio de bases paralelas iguales a los lados a y c. Trazando las diagonales de este trapecio y una paralela a las bases por el punto de encuentro de aquellas diagonales, determina un segmento cuya longitud es igual al doble de x. Consideramos, pues sólo su mitrad.

2. Sobre el lado BC=a, trazamos la circunferencia de diámetro igual al lado a=BC.

3. Trazamos la circunferencia de centro el punto B y radio x.

4. La intersección de las dos circunferencias anteriores nos determinará el punto C’. (el otro punto de corte proporcionaría una sol. simétrica).

5. Prolongamos el segmento BC’ hasta que coincida con el segmento dado, AB=c, obteniendo así el punto A, tercer vértice del triángulo buscado.