Problema
262
Propuesto
por Juan Bosco Romero Márquez, profesor colaborador
de
Hallar
todos los triángulos ABC con lados a,b
y c que tiene la propiedad que la mediana desde A, la bisectriz en B, y la
altura desde C, son concurrentes.
Guy (1995): My Favorite
Elliptic Curve : A Tale of Two Types of Triangles. The American
Mathematical Monthly (Vol.
102, No. 9 (1995), pages 771-781
Solución de Maite Peña Alcaraz, estudiante de Industriales
en
:
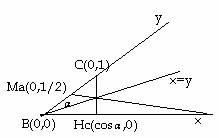
Tomemos
los puntos B y C en ese sistema de coordenadas. La altura de C sobre la recta x
es Hc y el punto medio de BC es Ma.
La bisectriz del ángulo B es la recta x=y. Si la mediana de A, la altura de C y
la bisectriz de B concurren, se cortarán en el punto P en el que se cortan la
altura de C y la bisectriz de B, cuyas coordenadas podemos calcular:
Y por tanto la longitud del
lado BC es 1, la longitud del lado AB es 
y el ángulo B mide 
. Luego para cada
ángulo , los triángulos de
lados proporcionales a 
estas medidas cumplirán la propiedad del
enunciado. Lo que es lo mismo, para cada
es un triángulo
que cumple las propiedades.