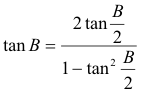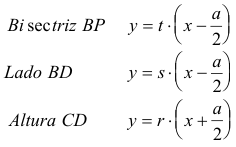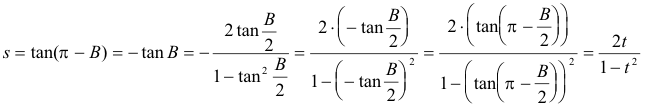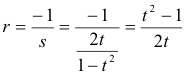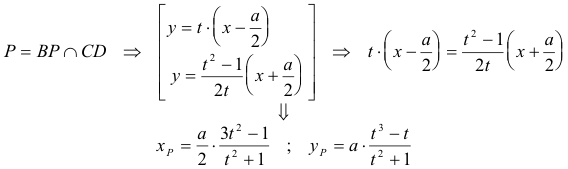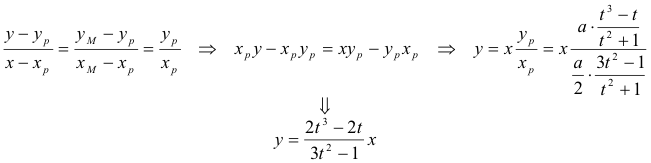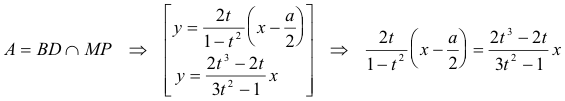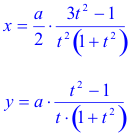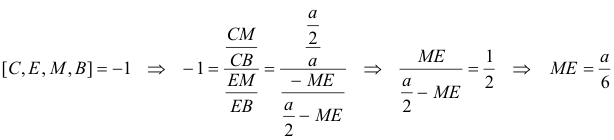Problema 262

Hallar todos los triángulos ABC con lados a, b y c que tiene la propiedad que la mediana desde A, la bisectriz en B, y la altura desde C, son concurrentes.

Guy (1995): My Favourite Elliptic Curve : A Tale of Two Types of Triangles. The American Mathematical Monthly (Vol. 102, No. 9 (1995), pages 771-781

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (8 de julio de 2005)

CONSTRUCCIÓN Y ESTUDIO SIMULTÁNEO

El enunciado nos habla de la perpendicular desde C al lado AB, suponemos que perpendicular y lado se cortan en el punto D. Este punto D es el vértice de un ángulo recto cuyos lados pasan por B y C. D estará sobre el círculo de diámetro BC.

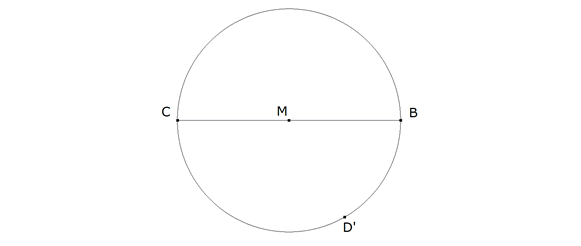
figura 1

Tomamos un segmento CB como base fija de los triángulos a determinar.

Con centro en M (punto medio de CB), trazamos el círculo de diámetro BC. Sobre este círculo tomamos un punto cualquiera D’ que consideraremos como pie de la perpendicular CD’ desde C al lado opuesto.

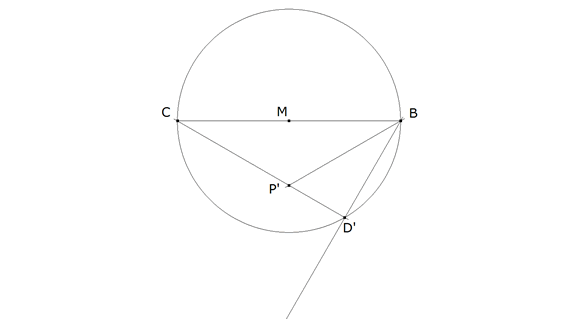
figura 2

El segundo lado del triángulo estará sobre BD’; lo que nos permite trazar la bisectriz del ángulo B.

Esta bisectriz corta a CD’ en P’.

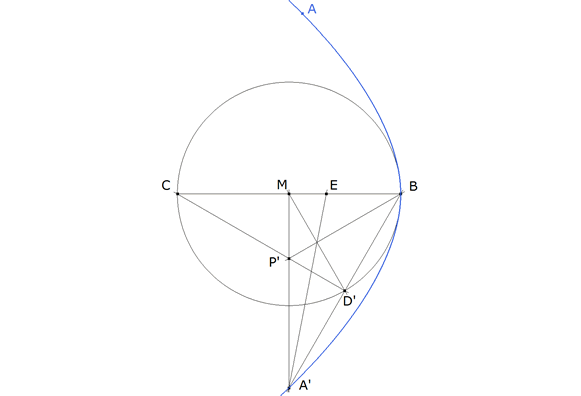
P’ ES EL PUNTO DE CONCURRENCIA MENCIONADO EN EL ENUNCIADO

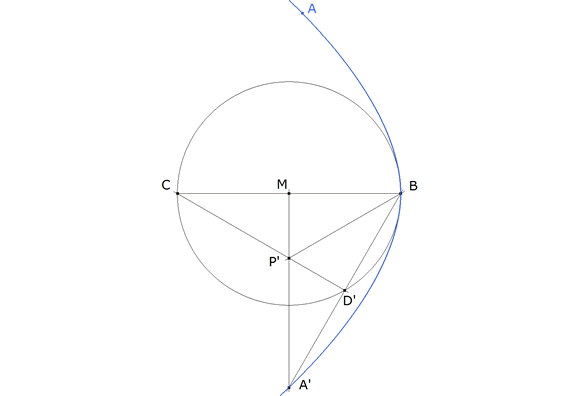
figura 3

Si la mediana del enunciado debe concurrir en P’, será la recta MP’. MP’ corta a BD’ en A’.

A’BC es uno de los triángulos buscados.

Si D’ se desplaza por su circunferencia obtenemos el lugar geométrico de los vértices A de los triángulos que cumplen las condiciones del enunciado.

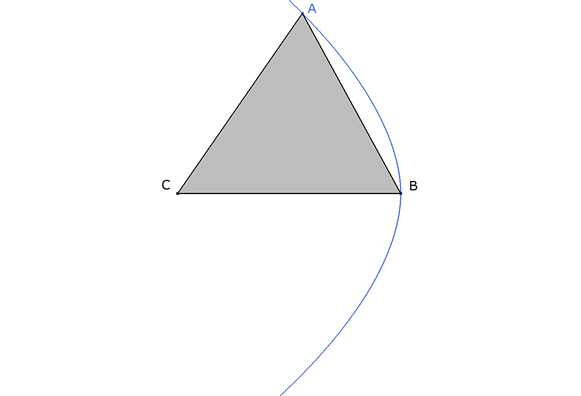
figura 4

Fijada la base BC, determinado el lugar geométrico anterior y tomando un punto cualquiera A sobre el lugar, podemos afirmar que el triángulo ABC así formado tiene concurrentes la mediana por A, la bisectriz por B y la altura por C.

HEMOS HALLADO UN MÉTODO QUE NOS PERMITE HALLAR CADA TRIÁNGULO

CON REGLA Y COMPAS

EL LUGAR GEOMÉTRICO NO PUEDE CONSTRUIRSE CON REGLA Y COMPÁS, EXCEPTO PUNTO A PUNTO

Si queremos partir del lugar geométrico trazado debemos determinar su ecuación.

LA ECUACIÓN DEL EL LUGAR GEOMÉTRICO DE LOS VÉRTICES A

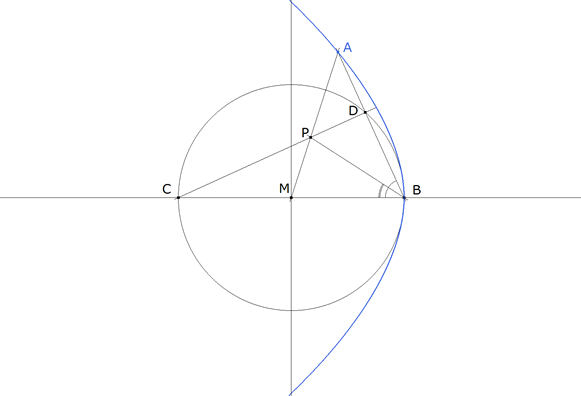
Consideremos de nuevo el método de construcción establecido. Vamos a ver que esta curva es una cúbica que posee una representación fácil si expresamos sus coordenadas dependiendo de un parámetro y elegimos convenientemente este parámetro. Usaremos un sistema de referencia con origen en M (punto medio de BC) y BC como eje de abscisas.

Como debemos considerar las rectas BD, BP, y CD, vale la pena elegir como parámetro la pendiente de una de esas rectas, Teniendo en cuenta la relación

vemos que es más fácil expresar la tangente en función del ángulo mitad, que expresar la tangente en función del ángulo doble y por eso tomaremos como parámetro la pendiente de la bisectriz BP

Después de esto podemos establecer las ecuaciones necesarias.

figura 5

Ecuaciones de las rectas

Como el ángulo del lado BD es el doble que el de la bisectriz, escribimos

Como la altura CD es perpendicular al lado BD

Vamos a hallar ahora el punto P

Podemos determinar ahora la mediana MP

Y ahora podemos obtener el vértice A

De donde obtenemos las siguientes ecuaciones para el lugar geométrico de los vértices A

UNA PROPIEDAD MÁS QUE PROPORCIONA OTRA CONSTRUCCION

figura 6

Si vemos la construcción básica (figura 6), M, B, D’, A’ con C y A’ forman un cuadrilátero completo. La recta desde A’ por la intersección de las diagonales BP’ y MD’ cortará a BC en E y por las propiedades del cuadrilátero completo

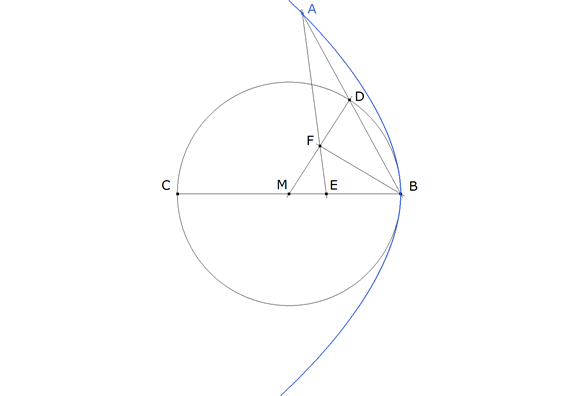
E SERÁ EL PUNTO ARMÓNICO DE C CON RESPECTO A M Y B

Pero ese punto armónico es fijo. Entonces al ser E fijo podemos simplificar la construcción.

figura 7

Iniciamos la construcción del mismo modo que la anterior.

Tomamos D sobre el círculo de diámetro BC. Trazamos la recta BD. Trazamos la bisectriz del ángulo B.

Aquí modificamos el método. Trazamos la recta MD que corta a la bisectriz en F. EF cortará a BD en A.

Se puede objetar que para trazar el punto armónico E debe trazarse un cuadrilátero completo; pero veamos que no hace falta (gracias a la razón doble de una cuaterna armónica)

¡ Qué es sencillísimo de construir !