Problema 264
Diez. Ejercicio 9: Supongamos que los puntos P y Q se encuentran sobre la circunferencia K descrita alrededor del triángulo ABC. Demostrar que el punto de intersección de las rectas correspondientes de Simpson p y q describe una circunferencia K' cuando A, B, P, Q están inmóviles y C recorre K. Lyúbich, Y.I., Shor, L.A. (1976, original ruso, 1978 edición en español. ). Método cinemática en problemas geométricos. Lecciones populares de matemáticas. Editorial Mir. Moscú. (traducción de Lozhkin, G.A.). (pág 51) Reseña: A veces, para resolver un problema geométrico, es útil imaginar las transformaciones que sufrirán los elementos de la figura a examinar, si algunos de sus puntos empiezan a desplazarse. La dependencia de unos elementos en función de otros puede pasar a ser evidente en este caso y la solución del problema saltará a la vista.
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (11 de julio de 2005) |
|
CONSTRUCCIÓN DE LA RECTA DE SIMPSON p |
|
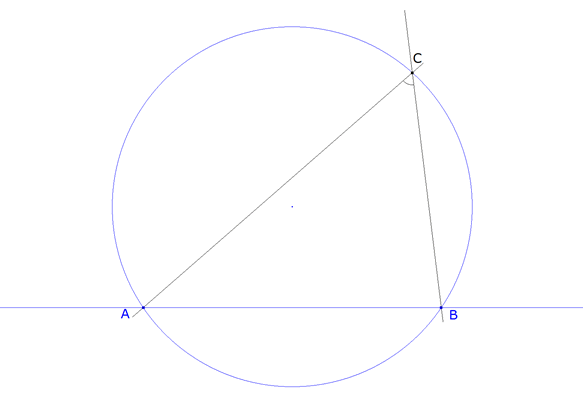
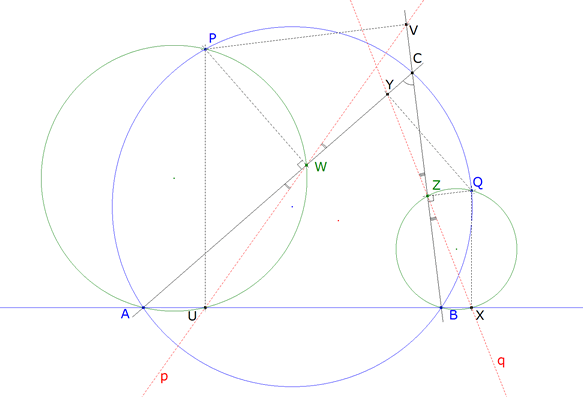
figura 1 Partiremos de un círculo cualquiera, que consideraremos como circunscrito a un triángulo ABC. Sobre dicho círculo colocamos tres puntos A, B y C. Consideraremos que A y B son fijos, mientras que C puede desplazarse sobre el círculo.
EN UN TRIANGULO ABC, FIJADA LA CIRCUNFERENCIA CIRCUNSCRITA Y BC
TEOREMA I Dado un triángulo ABC, las proyecciones de un punto cualquiera de la circunferencia circunscrita sobre los lados del triángulo están alineados en una línea recta llamada Recta de Simpson.
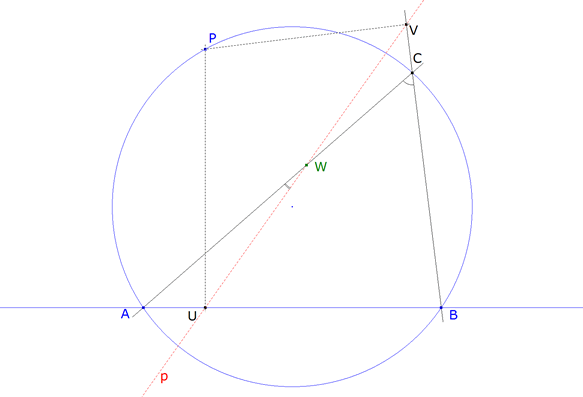
figura 2 Tomamos un punto cualquiera P sobre el circulo circunscrito. Consideraremos P como un punto fijo.
U ES UN PUNTO FIJO. Proyectamos (ortogonalmente) P sobre BC; obtenemos el punto V.
LUGAR GEOMÉTRICO DEL PUNTO W AL DESPLAZARSE C SOBRE SU CIRCULO
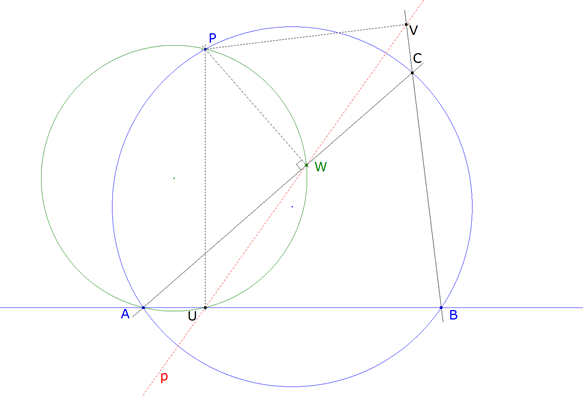
figura 3
EL LUGAR GEOMÉTRICO DE W ES LA CIRCUNFERENCIA DE DIÁMETRO AP
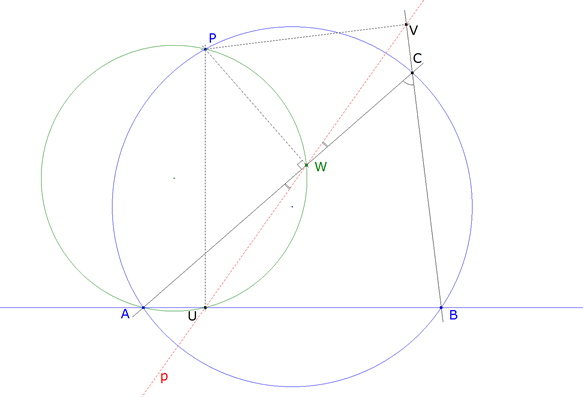
EL ÁNGULO AWU Y EL ÁNGULO CWV
figura 4
|
|
El PUNTO Q Y LA RECTA q |
|
figura 5 Al igual que con el punto P, tomamos un punto cualquiera Q fijo sobre el círculo circunscrito.
X ES UN PUNTO FIJO.
EL LUGAR GEOMÉTRICO DE Z ES LA CIRCUNFERENCIA DE DIÁMETRO BQ.
|
|
EL LUGAR GEOMÉTRICO DE LA INTERSECCIÓN DE p Y q |
|
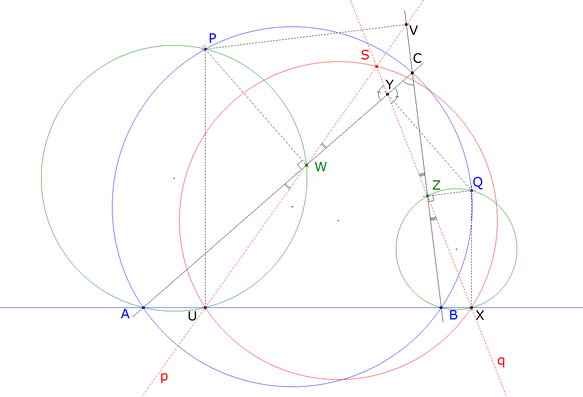
Obtenido S estudiemos el ángulo USX.
figura 6
El lado SU pasa por el punto fijo U y el SX por el punto fijo X.
¡ EL LUGAR GEOMÉTRICO DE S ES UNA CIRCUNFERENCIA QUE PASA POR U Y X !
|