Para el aula

Problema 265

Sea ABC un triángulo equilátero de centro O y lado 3.

Sea M un punto del lado AC tal que CM = 1 y sea P un punto del lado AB tal que AP = 1.

Calcula las medidas de los ángulos del triángulo MOP.

X Olimpíada Matemática Rioplatense San Isidro, 12 de Diciembre de 2001

Nivel A – Primer Día

http://www.oma.org.ar/enunciados/omr10.doc

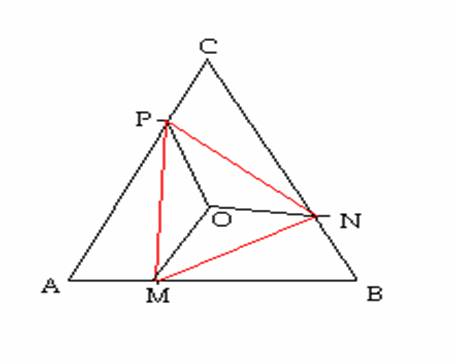
Sea M el punto que dista 1 de A y está en el segmento AB. Sea N el punto que dista 1 de B y está en el segmento BC. Sea P el punto que dista 1 de C y está en el segmento CA. Construyamos los triángulos MON, NOP y POM. Por construcción, OP=OM=ON y MN=NP=PM luego el nuevo triángulo MNP es equilátero, por lo que sus ángulos miden 60º. Como los lados OP, ON y OM son bisectrices del nuevo triángulo, el ángulo mide 30º y el ángulo también mide 30º, como en un triángulo, la suma de sus lados mide 180º, el ángulo tiene que medir 120º, por lo que esta es la medida de los ángulos del triángulo pedido.