Problema 265

Sea ABC un triángulo equilátero de centro O y lado 3.

Sea M un punto del lado AC tal que CM = 1 y sea P un punto del lado AB tal que AP = 1.

Calcula las medidas de los ángulos del triángulo MOP.

X Olimpíada Matemática Rioplatense San Isidro, 12 de Diciembre de 2001

Nivel A – Primer Día

http://www.oma.org.ar/enunciados/omr10.doc

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (11 de julio de 2005)

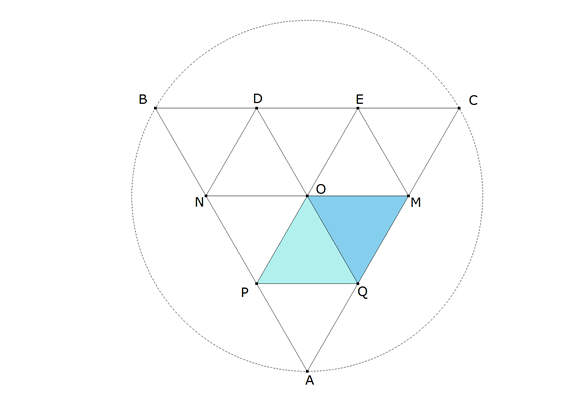
figura 1

Partiremos de un triángulo cualquiera ABC. Si el triángulo es equilátero de lado 3 y los segmentos del enunciado son 1, podemos decir que los segmentos son la tercera parte del lado. Dividimos entonces cada lado del triángulo equilátero en tres segmentos iguales.

Sean P, N los puntos que dividen a AB en tres segmentos iguales.

Sean D, E los puntos que dividen a BC en tres segmentos iguales.

Sean M, Q los puntos que dividen a CA en tres segmentos iguales.

Sabemos entonces que

PQ y NM son paralelas a BC (por ejemplo, la división en partes iguales nos dice que APQ y ABC son homotéticos).

ND y PE son paralelas a CA.

ME y QD son paralelas a AB.

figura 2

Al ser todas las divisiones iguales y todas las rectas paralelas a los lados respectivos tenemos que todos los triángulos formados son equiláteros y por tanto