Problema 267
Desde cada vértice de un triángulo ABC se trazan dos segmentos que se unen con puntos del lado opuesto de manera que lo dividen en tres segmentos de igual longitud. Estas seis líneas determinan un hexágono.
Demostrar que las tres diagonales que unen los vértices opuestos de ese hexágono tienen un punto en común.

Yaglom IS(1962). Geometric Transformations III.
The Mathematical Association of America (MAA) New Matematical Library (p. 5)
(Traducido del ruso por Allen Shields).

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba, España.

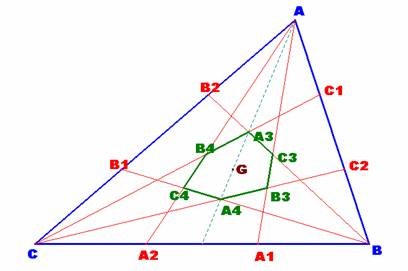
Dado el triángulo ABC siguiente, señalamos en él los puntos de subdivisión en cada uno de sus lados. Señalamos los siguientes hechos de interés:

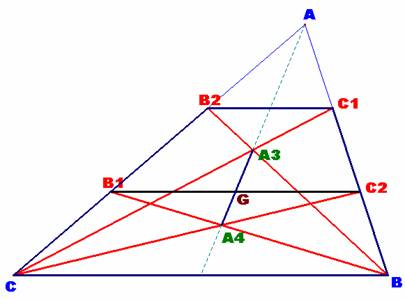
1.- El cuadrilátero B₁C₂BC es un trapecio de bases, B₁C₂ y BC, respectivamente.

Sus diagonales se cortan en el punto A₄, que está alineado con el vértice A y el punto medio del lado BC, es decir, el punto A₄ pertenece a la mediana m_a.
(Ver para más detalle el ejercicio 259).

2.- El cuadrilátero B₂C₁BC es un trapecio de bases, B₂C₁ y BC, respectivamente.

Sus diagonales se cortan en el punto A₃, que está alineado con el vértice A y el punto medio del lado BC, es decir, el punto A₃ pertenece a la mediana m_a.
(Ver para más detalle el Problema 259).

De las consideraciones anteriores, deducimos que el segmento A₃A₄ pertenece a la mediana m_a. Por razones de simetría, el punto G, baricentro del triángulo ABC debe ser un punto interior del segmento A₃A₄.

Usando el mismo razonamiento anterior, con las otras dos medianas, m_b y m_c, deducimos que, en efecto, las tres diagonales que unen los vértices opuestos de aquél hexágono tienen un punto en común, G, baricentro del triángulo ABC.