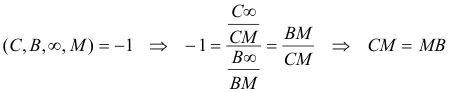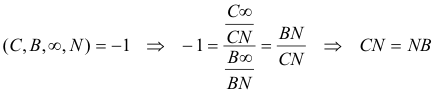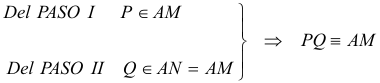Problema 267

8. Desde cada vértice de un triángulo ABC se trazan dos segmentos que se unen con puntos del lado opuesto de manera que lo dividen en tres segmentos de igual longitud. Estas seis líneas determinan un hexágono.

Demostrar que las tres diagonales que unen los vértices opuestos de ese hexágono tienen un punto en común.

Yaglom IS(1962) Geometric Transformations III The Mathematical Association of America (MAA) New Matematical Library (p. 5) (Traducido del ruso por Allen Shields)

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (11 de julio de 2005)

INTRODUCCION

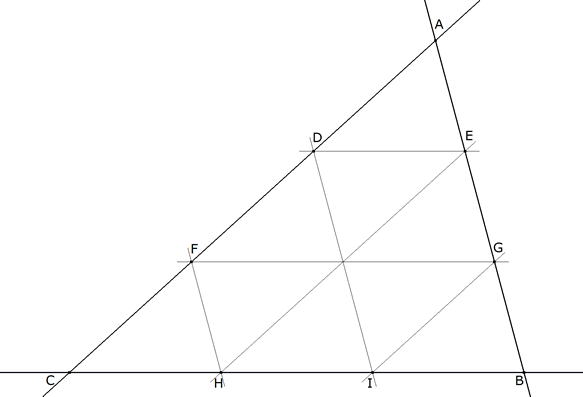
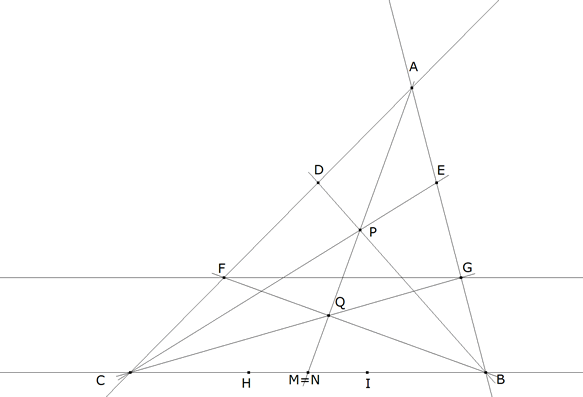
TRIANGULO DEL ENUNCIADO

figura 1

Partiremos de un triángulo cualquiera ABC.

Sean H, I los puntos que dividen a BC en tres segmentos iguales.

Sean D, F los puntos que dividen a CA en tres segmentos iguales.

Sean E, G los puntos que dividen a AB en tres segmentos iguales.

Sabemos entonces que

DE y FG son paralelas a BC (por ejemplo, la división en partes iguales nos dice que ADE y ACB son homotéticos).

GI y EH son paralelas a CA.

FH y DI son paralelas a AB.

Establecido lo anterior, no estudiaremos la figura completa. Estudiaremos sólo la construcción de una parte que nos proporcionará lo suficiente para responder al enunciado.

Tomamos como referencia el lado BC y empezamos a construir el enunciado sólo en parte.

CONSTRUCCION - CONSIDERAMOS LOS VÉRTICES BC

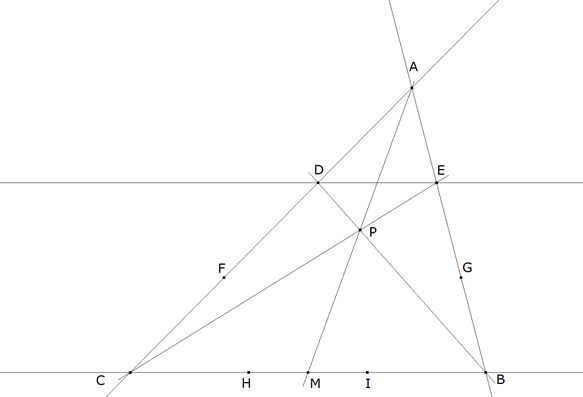
PASO I

figura 2

Trazamos BD y CE, recordemos que DE es paralela a CB

BCDE con A y ∞ es un cuadrilátero completo. BD y CE son sus diagonales interiores. Los lados CD y EB se cortan en A y las diagonales interiores en P; entonces por las propiedades del cuadrilátero

AP encuentra a BC en M; se cumple pues

De donde M es el punto medio de BC y por tanto

LA RECTA AP COINCIDE CON LA MEDIANA POR A

PASO II

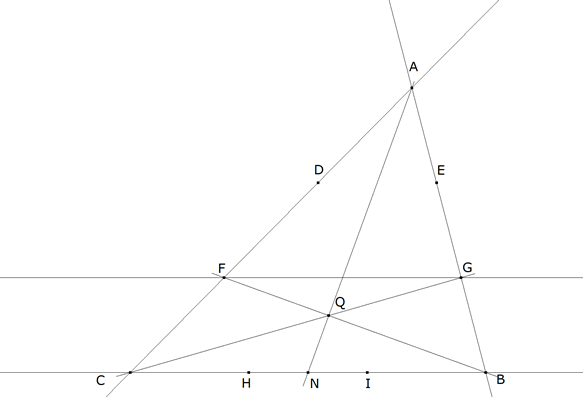
figura 3

Trazamos BF y CG, recordemos que FG es paralela a CB

BCFG con A y ∞ es un cuadrilátero completo. BF y CG son sus diagonales interiores. Los lados CF y GB se cortan en A y las diagonales interiores en Q; entonces por las propiedades del cuadrilátero

AQ encuentra a BC en N; se cumple pues

De donde N es el punto medio de BC y por tanto

LA RECTA AQ COINCIDE CON LA MEDIANA POR A

CONCLUSIÓN

Hemos visto que M y N coinciden con el punto medio de BC, por lo tanto

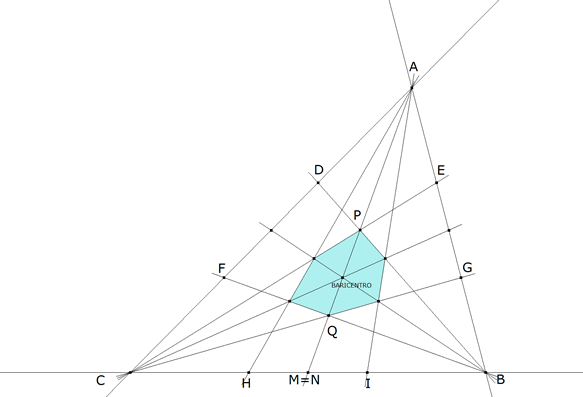
figura 4

Pero siguiendo el enunciado PQ es una de las diagonales del exágono. Podemos pues concluir que:

LAS TRES DIAGONALES DEL EXÁGONO SON LAS TRES MEDIANAS DEL TRIÁNGULO

Y POR TANTO SON CONCURRENTES EN EL BARICENTRO

figura 5