Problema 268.

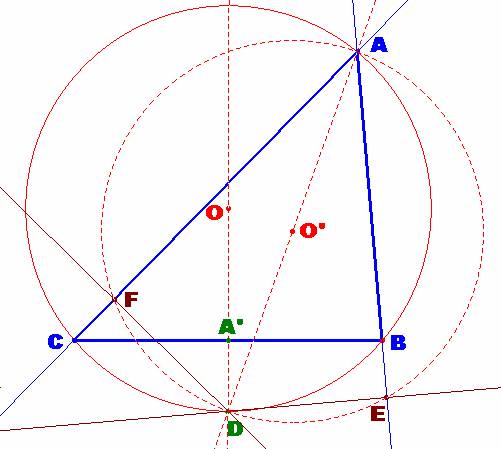
Dado un triángulo ABC se traza la circunferencia circunscrita K. Se traza la bisectriz de A que corta a K en D. Tracemos las perpendiculares desde D, DE a AB y DF a AC.
Demostrar que:
1.- E y F están en distinta posición respecto a K.
2.- Si ambos están sobre la K, ¿cómo es ABC?
3.- Los segmentos EB y CF miden igual.

Barroso, R. (2004): Comunicación personal.
Videoconferencia con Iberocabri. Saltillo, Cohauila, Méjico(4 de junio)

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba, España.

1.- E y F están en distinta posición respecto a K.

A, D, E y F están situados en la circunferencia de diámetro, la cuerda AD. Por tanto, al tener ambas circunferencias dos puntos en común, A y D, la posición relativa de ellas hace que un punto esté en el interior de una y el otro en el exterior por pertenecer dichos puntos a semiplanos diferentes respecto del diámetro AD.

2.- Si ambos están sobre la K, ¿cómo es ABC?

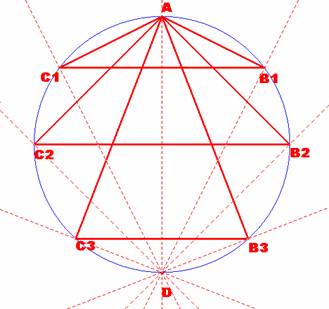
Si ambos puntos están sobre la misma circunferencia K, el triángulo ABC deberá ser isósceles como se muestra en la siguiente figura. Como ya se ha indicado en el apartado anterior, la cuerda AD ejercerá como diámetro de la nueva circunferencia y para evitar que los puntos E y F sean uno interior y otro exterior a la misma, deberán pertenecer ambos a la primera circunferencia K y así coincidirán con los vértices Bi y Ci, respectivamente. Esto sucederá únicamente cuando la bisectriz del ángulo A coincide con su misma altura, es decir, que el triángulo ABC sea isósceles en A.

3.- Los segmentos EB y CF miden igual.

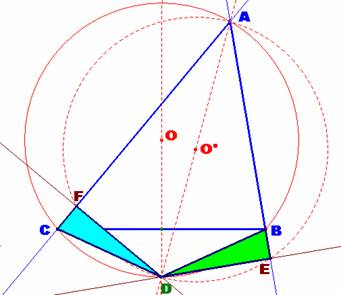
Examinemos los triángulos rectángulos DFC y DEB. * Ambos tienen dos lados iguales, DF = DE, por tratarse de dos lados homólogos en el par de triángulos congruentes AFD y AED. *También tienen otro par de lados iguales, CD = BD, por pertenecer el punto D a la mediatriz del segmento BC. De esta manera, el otro par de lados también deberán ser iguales, EB = CF.