Problema 268.

Dado un triángulo ABC se traza la circunferencia circunscrita K.

Se traza la bisectriz de A que corta a K en D.

Tracemos las perpendiculares desde D, DE a AB y DF a AC.

Demostrar que:

1.- E y F están en distinta posición respecto a K.

2.- Si ambos están sobre la K, ¿cómo es ABC?

3.- Los segmentos EB y CF miden igual.

Barroso, R. (2004): Comunicación personal. Viedoconferencia con Iberocabri. Saltillo, Cohauila, Méjico(4 de junio)

SOLUCIÓN

1er caso

Partiremos suponiendo que los puntos E y F están en la parte interior a la circunferencia

Luego observamos que los segmentos BD y DC son iguales Ahora como el cuadrilátero ABDC es inscriptible los ángulos EBD y DCK serán iguales pero nos damos con la sorpresa que en el triángulo EBD es ángulo a es agudo y en el triángulo DFC el mismo ángulo es obtuso por lo tanto la perpendicular DF tendrá que caer fuera de la circunferencia sobre el siento CK para que el ángulo sea agudo

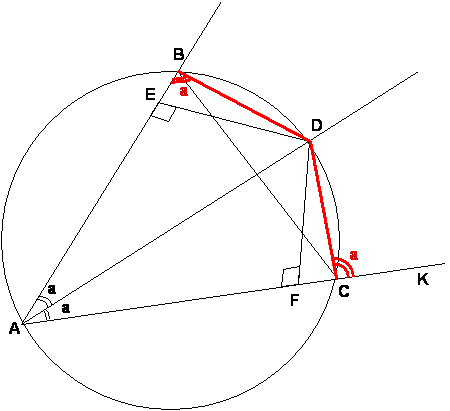
Con lo que demostramos que los puntos E y F uno cae dentro de la circunferencia mientras que el otro en la parte externa.

2do caso

La única posibilidad es que la bisectriz sea el diámetro para que los puntos E y F coincidan en la circunferencia pues el cuadrilátero ABDC es inscriptible.

3ra caso

Como los triángulos rectángulos BED y DFC son congruentes entonces los segmentos EB y CF son iguales