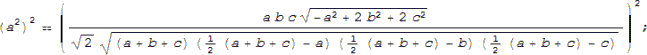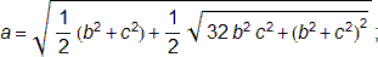Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 270. Un triángulo ABC, verifica entre uno de sus lados a, la mediana correspondiente a ese lado ma, y el radio del círculo circunscrito R, la relación: a^2 = 4 R ma.

Probar si es cierto o no que aparte de los triángulos rectángulos en A, hay, al menos otro.

Romero, J.B. (2005): Comunicación personal (Dedicado a Murray S. Klamkin)

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (11 de julio de 2005)

INTRODUCCION

RELACIÓN ENTRE LA MEDIANAS Y LOS LADOS

EXPRESIÓN DEL RADIO CIRCUNSCRITO EN FUNCIÓN DE LOS LADOS Y EL SEMIPERÍMETRO

ECUACIÓN DEL ENUNCIADO

SOLUCIÓN

PASO I

En la ecuación del enunciado, sustituimos R y ma en función de los lados

PASO II

Eliminamos raíces y denominadores e igualamos a cero

PASO III

Simplificamos y descomponemos en factores

PASO IV

El primer factor sería el trivial

El segundo factor es el del triángulo rectángulo

El tercer factor es una bicuadrada en a que sólo posee una solución real y positiva