Problema 270

Un triángulo , verifica entre un de su lado, a, la mediana correspondiente al lado a y el radio del círculo circunscrito R, la relación:

.

Probar si es cierta o no que a parte de los triángulos rectángulos en A, hay otros.

Solución:

Nota: Si el triángulo es rectángulo , entonces , .

Entonces se cumple la relación .

Supongamos que se cumple la relación: .

Aplicando el teorema de los senos al triángulo :

.

. Simplificando:

.

Entonces la relación se cumplirá cuando:

Elevando al cuadrado la inecuación:

Aplicando la fórmula de la mediana en función de los lados:

.

. Simplificando:

, Entonces, el ángulo A es recto o obtuso.

Como resolverlo con regla y compás partiendo de a y :

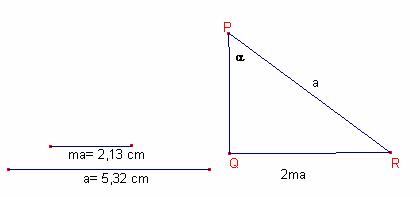
a) Dibujar un triángulo rectángulo de hipotenusa a y cateto , ().

Sea . Entonces,

b) Dibujar el lado .

c) Dibujar el punto medio M del lado .

d) Dibujar sobre el lado el arco capaz de :

e) Dibujar la circunferencia de centro M y radio que corta el arco capaz en el punto A.

f) Dibujar el triángulo que cumple las hipótesis del problema.

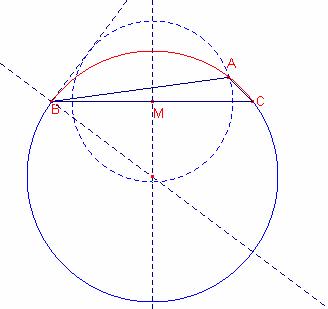
Prueba con Cabri:

Figura barroso270b.fig

Applet created on 2/09/05 by Ricard Peiró with CabriJava