Problema 270.-

Un triángulo ABC, verifica entre uno de sus lados, a, la mediana correspondiente a ese lado m_a, y el radio del círculo circunscrito R, la relación:

                a² = 4 R m_a. (1)

Probar si es cierto o no que aparte de los triángulos rectángulos en A, hay, al menos otro.

Romero, J.B. (2005): Comunicación personal (Dedicado a Murray S. Klamkin)

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León (Salamanca)..-

La relación (1) puede expresarse de otro modo sustituyendo 2R por .

a² = 4 R m_a. (1) se transforma, después de simplificar, en 2·m_a = a·sen A (1’)

Sea a < 2R. La construcción del triángulo a partir de los tres datos, lado a, mediana correspondiente m_a y radio R de la circunferencia circunscrita es inmediata e única, salvo movimientos.

Sobre la circunferencia de radio R se toma una cuerda BC de longitud a. Desde el punto medio de ella un arco de radio m_a determina el vértice A que falta para completar la construcción del triángulo, (hay otro corte con el que se construye un triángulo simétrico).

En el caso particular de coincidir el valor de a con el diámetro de la circunferencia circunscrita, el ángulo opuesto A es recto y la mediana coincide con el radio. La construcción anterior no sirve; cualquier punto de la circunferencia puede tomarse como vértice A, y hay infinitas soluciones. Si excluimos este caso, utilizando la fórmula del enunciado, sólo necesitamos dos datos:

1.- Si tenemos a y R o a y m_a, el segmento que falta se construye fácilmente a partir del teorema de Thales, expresando la relación (1) del enunciado como .

2.- Si nos dan R y m_a tenemos que a es el doble de la media proporcional de ambos.

Cálculo de la mediana en función de los lados.

Veamos cómo calcular la mediana de un triángulo en función de los lados del mismo.

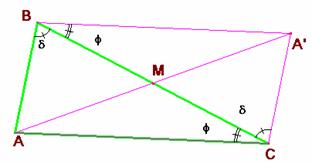
El segmento AA’ es igual a 2·m_a. Según el teorema del coseno para el triángulo AA’C se tiene:

(2·m_a)² = b² + c² – 2·bc·cos(f +d). (2)

En la figura adjunta podemos ver que el ángulo A del triángulo ABC es el suplemento de f +d, y por ello sus cosenos son opuestos, pudiendo poner:

(2·m_a)² = b² + c² +2·bc·cos A. (3)

Como por otra parte tenemos a² = b² + c² – 2·bc·cos A (4) sumando ambas eliminamos el coseno quedando

(2·m_a)² + a²= 2(b² + c²) (5)

que permite el cálculo de la mediana a partir de los lados.

Para a < 2R los triángulos que verifican (1) son obtusángulos.

Excluido el triángulo rectángulo, todos los triángulos que verifican la relación (1) son obtusos en A.

Restando (3) y (4) elimina b² + c² y nos queda (2·m_a)² = a² + 4 bc·cos A.

Usando ahora (1’) podemos poner (a·sen A) ²= a² +4 bc·cos A.

Después de simplificar (cos A0) queda

–a²· cos A = 4 bc (6)

expresión que nos indica que el ángulo A es mayor de 90º, pues su coseno es negativo. c.q.d.