Problema 271

Problema 80. Distancias en el triángulo. Dibuje un triángulo equilátero de 10 cm de lado y señale cinco puntos en su interior.

¿Sabría razonar que en cualquier caso habrá siempre dos puntos que están como máximo a 5 cm de distancia?

Deulofeu, J. (2001): Una recreación matemática : historias, juegos y problemas.
Planeta Prácticos. Barcelona (pag 76)

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba, España.

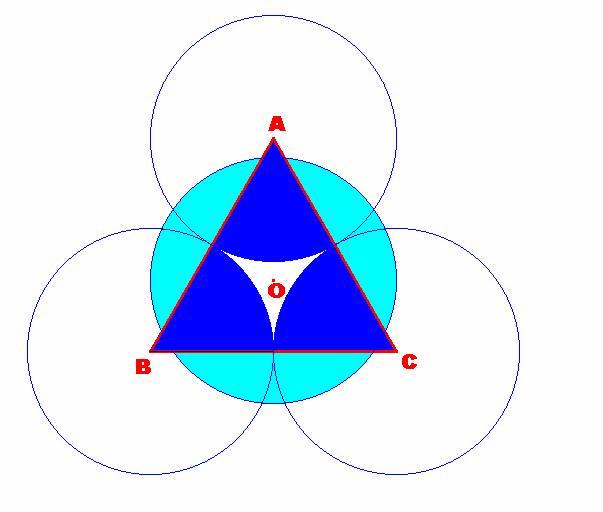
Dado el triángulo equilátero ABC, de lado igual a 10 cm, situamos tres puntos haciéndolos coincidir en su posición límite con los vértices A, B y C. De este modo, el cuarto punto deberá estar situado en la región interior limitada por los tres arcos de circunferencia de radio igual a 5 cm. Sea este el punto O. Así ya el quinto punto deberá pertenecer a la circunferencia de centro el punto O y de radio 5 cm, que como se ve en la figura, o bien contiene a las regiones de “influencia” de los puntos A, B y C, o bien queda fuera del triángulo inicial. Por tanto, en efecto, habrá siempre dos puntos que están situados como máximo a 5 cm de distancia.