Problema 272
Una línea recta que pasa por el incentro de un triángulo ABC
corta a los lados AB y AC en los puntos D y E respectivamente. Sea P el punto
de intersección de BE y CD.
Si X, Y y Z son los respectivos pies de las perpendiculares desde P a BC, CA y
AB, demuestre que:
1/PX
= 1/PY + 1/PZ
Propuesto por el profesor José Manuel
Arranz San José, profesor de Educación Secundaria de Ponferrada (León).
Oposiciones Secundaria (2005) Baleares.
Solución
de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba,
España.
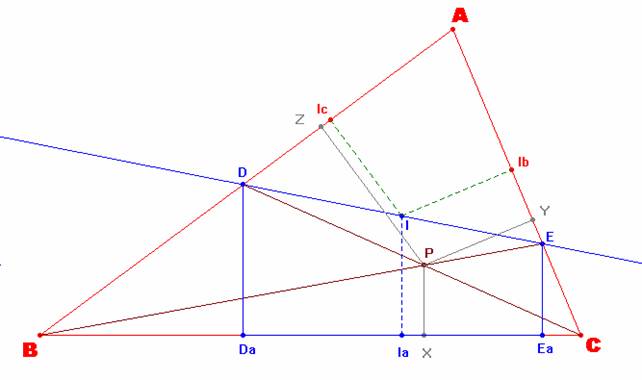
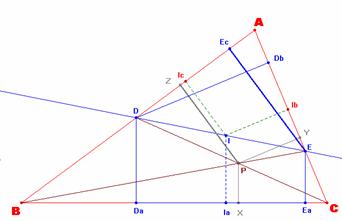
Sea la anterior configuración, donde
hemos trazado las perpendiculares desde los puntos D y E hasta el lado BC,
siendo Da y Ea, sus respectivos pies. Así que podemos
ahora realizar las siguientes consideraciones:
·
El punto P divide al segmento BE en la razón [m:1].
Es decir, ![]()
·
El punto P divide al segmento CD en la razón [n:1].
Es decir, ![]()
·
El punto I, Incentro del triángulo ABC, divide al segmento DE en la razón [p:1].
Es decir, ![]()
|
RELACIONES QUE DETERMINAN EL VALOR DE
PX EN FUNCIÓN DE m, n, p y r. |
|
Con el par de
triángulos semejantes BPX y BEEa, tenemos que: Con el par de
triángulos semejantes CPX y CDDa, tenemos que: Así que: |
|
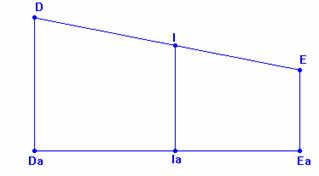
Consideramos
ahora el trapecio DEEaDa y notamos su área como [DEEaDa]
. Tenemos que: [DEEaDa]=
[DIIaDa]+ [IEEaIa];
Si dividimos por IaEa y simplificamos llegamos a obtener las
siguientes expresiones:
|
Con estas razones podemos
establecer las siguientes relaciones de interés:
|
|
|
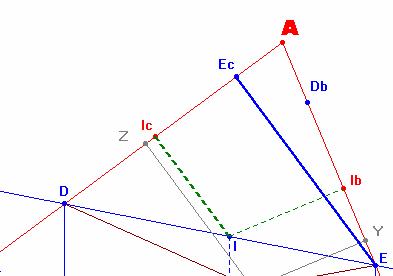
Veamos ahora las siguientes
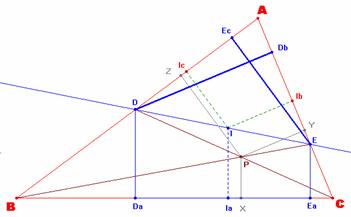
situaciones que nos propician las expresiones de PY y PZ. Si trazamos las perpendiculares
desde el punto D y E hasta los lado AC y BC respectivamente, obtenemos los
puntos Db y Ec.
|
|
|
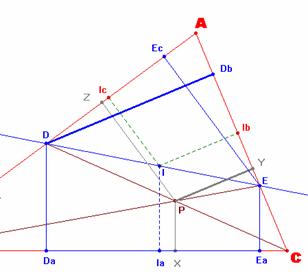
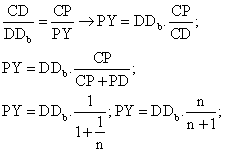
Sea el siguiente par de
triángulos semejantes CDDb
e CPY. Tenemos ahora que:
|
|
|
Sea el siguiente par de
triángulos semejantes BEEc
y BPZ. Tenemos ahora que:
|
|
|
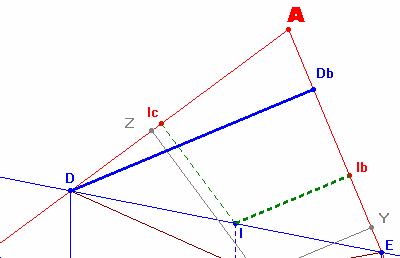
Si ahora trazamos la
perpendicular desde el punto D hasta el lado AC obtenemos el punto Db
y el siguiente par de triángulos semejantes DEDb e IEIb. Tenemos ahora que:
|
|
|
Si trazamos la perpendicular
desde el punto E hasta el lado AB obtenemos el punto Ec y el
siguiente par de triángulos semejantes DEEc y DIIc. Tenemos ahora que:
|
|
De estas cuatro últimas
igualdades:
Por lo tanto, la suma requerida
será: |
|
|
De ambas expresiones (I) y
(II), concluimos que: |
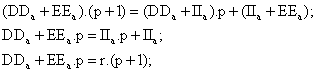

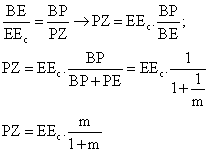

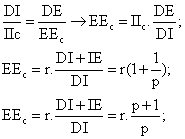
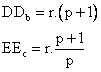 obtenemos que: DDb = p∙EEc
obtenemos que: DDb = p∙EEc
