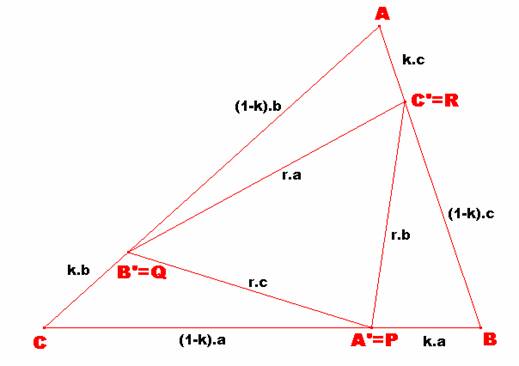
Problema 273

P, Q, R denotan puntos sobre los lados BC, CA y AB, respectivamente, de un triángulo dado ABC.
Determinar todos los ABC tales que si  BP/BC = CQ/CA = AR/AB = k  (distintos de 0, 1/2) entonces PQR (en este orden) es semejante a ABC.

Este problema aparece en Crux Mathematicorum (llamada en esas fechas Eureka) en Vol.3, 1977, January, No.1.
Klamkin.S. (1977): Eureka. Vol 3. Januay. N1. Problema 210 (Revista predecesora de Crux Mathematicorum)

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba, España.

Sea el triángulo ABC de la figura con las características del enunciado.

 

Si r es la razón de semejanza entre ambos triángulos ABC y A’B’C’, entonces la razón entre sus áreas será igual a r2. Sea S el área del triángulo ABC,  [ABC]=S.
Por un lado, será [A'B'C']=S×r2.

Por otra parte y como se quiera que [AB'C'] = [A'BC'] = [A'B'C] = k×(1-k)×S, tenemos que: [A'B'C']=S-3× k×(1-k)×S =S× (3k2-3k+1)

En definitiva, 3k2-3k+1= r2.

Buscamos ahora otra relación entre r2 y  k.
Si usamos el Teorema del Coseno en los triángulos AB'C' y ABC, obtenemos las siguientes identidades:

r2×a2 = (1-k)2×b2 + k2×c2 - 2×(1-k)×b×k×c×cosA
a2 = b2 + c2 - 2×b×c×cosA

Igualando las expresiones de cos A, y simplificando obtenemos:

;    

Por tanto,

 

r2 ∙a2 = 3k2∙a2-3k∙a2+a2

 

Igualando ambas expresiones, llegamos a la siguiente expresión algebraica en k:

 

k2 ·(4·a2  − 2·(b2  + c2 )) − k·(4·a2  − 3·b2  − c2 ) + a2 − b2  = 0,     

Como sabemos que una de las raíces es k=1/2, la factorización es igual a:

(2·k − 1)·(k·(2·a2 − b2 − c2) − a2 + b2) = 0 , y como por hipótesis k¹1/2, entonces:         

(k·(2·a2 − b2 − c2) − a2 + b2) = 0       (I)

 

Si usamos los valores de cos B y cos C, como antes ya lo hicimos con cos A, resultarían las siguientes expresiones:

 

(k·(2·b2 − c2 − a2) − b2 + c2) = 0       (II)

 

(k·(2·c2 − a2 − b2) − c2 + a2) = 0       (III)

 

Para que estas tres ecuaciones de primer grado (I), (II) y (III) tengan solución para cualesquiera valores de k¹0, k¹1/2, habrá de ocurrir que, simultáneamente, todos los coeficientes sean nulos. Por lo que resultaría:

 

;        

;

;

 

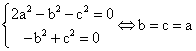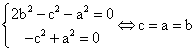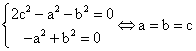En resumen, sólo los triángulos equiláteros ABC verifican dicha propiedad.