Problema 274.- 1) Sea X un punto arbitrario del triángulo ABC. Construimos los puntos C´, B´, A´, como los centros de gravedad de los triángulos ABX AXC y BXC. Sea X* el punto de intersección de las rectas AA´, BB´ y CC´. Se pide :

a) El triángulo A´B´C´ es homotético al triángulo ABC. Calcular el centro y la razón de la homotecia.

b) Si G y G´ son los centros de gravedad de los triángulos ABC, y A´B´C´, respectivamente, probar que los puntos G, G´, X y X* son colineales, y, calcular su razón doble.

Romero, J.B. (2005): Comunicación personal

Solución de Saturnino Campo Ruiz,, profesor del IES Fray Luis de León, de Salamanca..-

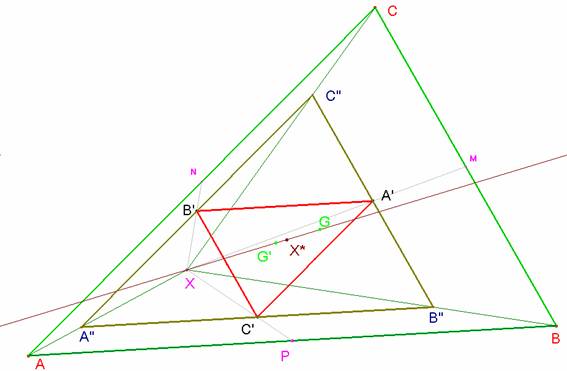
a)Trazando paralelas por A,’B’ y C’ a los lados del triángulo ABC se construye el triángulo A”B”C”. Se pasa de uno a otro por una homotecia de centro X y razón 2/3. P, punto medio de AB, se transforma en C’ punto medio de A”B”, y por ello A”B”C”es homotético a A’B’C’ por una homotecia de centro G’, el baricentro de ambos, y razón -1/2.

La composición de estas homotecias es otra homotecia de ABC en A’B’C’. Su centro es el punto X* y su razón -1/3 (el producto de las razones de los factores). Además, los centros de las tres homotecias, puntos X, G’ y X*, están alineados.

b) Como en una homotecia son homólogos los baricentros, resulta que G y G’ están alineados con X y por tanto ya tenemos la alineación de los cuatro puntos que buscábamos. La razón doble (G G’ X X*) es el cociente de las razones simples (XGG’) y (X*GG’). La primera vale 3/2 (razón de paso de A”B”C” a ABC) y la segunda -3 (igual de A’B’C’a ABC ). Por tanto el valor de esa razón doble es -1/2.