Problema 275

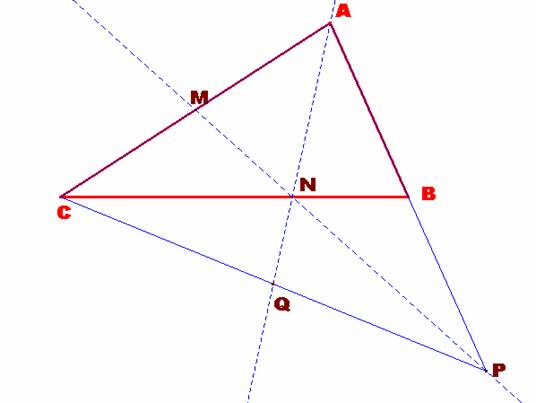
En un triángulo ABC, M es el punto medio del lado AC y N es el punto del lado BC tal que CN = 2BN. Si P es el punto de intersección de las rectas AB y MN, demuestra que la recta AN corta al segmento PC en su punto medio.

Para el aula.
X Olimpíada Matemática Rioplatense ( San Isidro, 12 de Diciembre de 2001)
(Nivel I – Primer Día)

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba, España.

La transversal MN determina el punto P en el lado AB y por el Teorema de Menelao tenemos que se verifica la relación: .

Sustituyendo sus valores tenemos que:

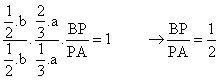
El punto B es el punto medio del segmento AP.
Como el punto N divide a la mediana CB según la razón 3:1, se tiene que N es el baricentro del triángulo APC. Consecuentemente, la ceviana que parte del vértice A y pasa por el baricentro N intercepta al lado opuesto PC en su punto medio.

Luego la recta AN corta al segmento PC en su punto medio.