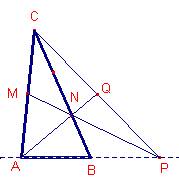
Problema 275

01. En un triángulo ABC, M es el punto medio del lado AC y N es el punto del lado BC tal que CN = 2BN. Si P es el punto de intersección de las rectas AB y MN, demuestra que la recta AN corta al segmento PC en su punto medio.

X Olimpíada Matemática Rioplatense ( San Isidro, 12 de Diciembre de 2001)(Nivel I – Primer Día)

Solución de Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València):

, . Siga

La recta MN corta la continuación del lado en el punto P.

Aplicando el teorema de Menelao al triángulo :

.

Entonces:

Sea el punto Q intersección de la recta AN y la recta PC.

Los segmentos , , son tres cevianas del triángulo que se cortan los tres en el punto N. Aplicando el teorema de Ceva al triángulo :

Como :

Entonces, Q es el punto medio del segmento .

Con Cabri:

Figure barroso275.fig

Applet created on 2/10/05 by Ricard Peiró with CabriJava