Problema 276
Para el aula.

Circunferencias y tangencias.
O es un punto sobre la circunferencia circunscrita al triángulo ABC.
Demostrar que si las perpendiculares desde O a los lados AB, AC y BC cortan a la circunferencia en los puntos c, b y a, el triángulo abc es igual en todos los aspectos al ABC.
[Nota del director: tienen los mismos lados y ángulos, aunque el orden es diferente]

a)Estudiar a qué transformaciones se somete ABC para transformarse en el abc, de manera que se solapen exactamente [añadido por el director].

Aref, M.N., Wernick,W. (1968): Problems &Solutions in Euclidean Geometry. Dover Publications, Inc, New York. (pag. 97)

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba, España.

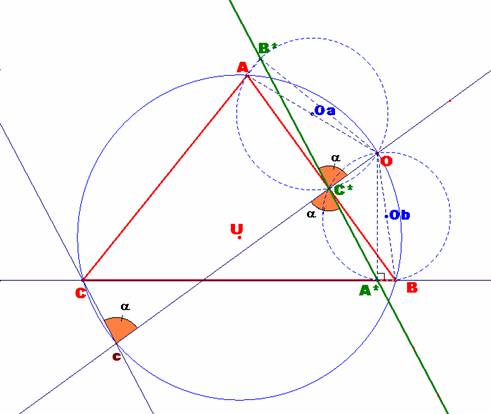
a) Para el punto O dado, construimos su recta de Simson. Procederemos, pues, desde el punto O a trazar perpendiculares a los lados del triángulo ABC, obteniendo los puntos A*, B* y C*. La recta de Simson será la que contiene a estos puntos. Será la recta coloreada en verde de la fig.1.

Figura 1

Tal como se indica en el enunciado, construimos los puntos a, b y c.
Consideramos ahora uno de ellos, sea el punto c.
Probaremos que las rectas Cc y la de Simson son paralelas. Para ello vemos que los ángulos que determinan con la transversal Oc son iguales.

Vemos esto con mayor detalle:

ÐOcC = a, ángulo inscrito en la circunferencia de centro U y que abarca el arco

ÐCBO = a por ser también un ángulo inscrito en la misma circunferencia y que abarca el mismo arco .

Pero el ángulo ÐCBO = a, es también un ángulo inscrito en la circunferencia de centro O_b y de diámetro OB. Por tanto en el triángulo rectángulo OA*B, el ángulo ÐA*OB = p/2 −a . Pero ahora tenemos que ÐA*OB = ÐA*C*B =p/2 −a, ya que ambos ángulos están inscritos en la misma circunferencia y abarcan el mismo arco . Como las rectas AB y Oc son perpendiculares, entonces ÐcC*A* ==p/2 −(p/2 −a) = a .

De esta manera, la mediatriz de la cuerda Cc pasará por el centro U de la circunferencia y será perpendicular a la Recta de Simson.

De igual modo podíamos haber probado que las mediatrices de las cuerdas Bb y Aa pasan por el centro U de la circunferencia y ambas serán igualmente perpendiculares a la Recta de Simson. Como esta Recta está determinada para la posición del punto O, resultará que el triángulo abc será el transformado del ABC por la simetría de eje, la recta perpendicular a la Recta de Simson por el centro U de la circunferencia circunscrita al triángulo ABC.

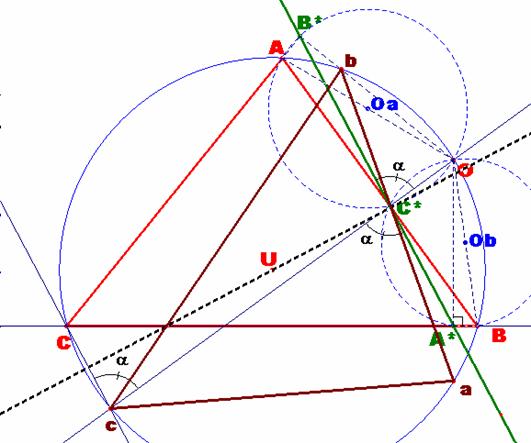
Como quiera que el eje de simetría es un diámetro, resultará que el triángulo abc será semejante al inicial ABC pero con distinta orientación. Ver fig.2.

Figura 2

b) Si ahora repetimos para el triángulo abc la misma transformación respecto al mismo punto O, obtendremos un nuevo triángulo a’b’c’ que tendrá la misma orientación que le inicial ABC y por tanto mediante un giro centrado en el punto U podemos hacer que se solapen ABC y el nuevo triángulo girado a’’b’’c’’.