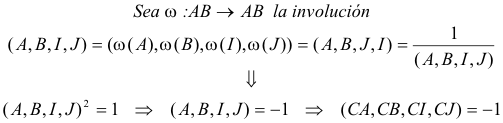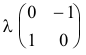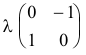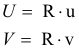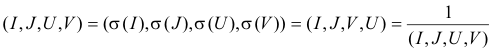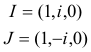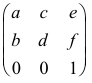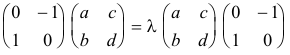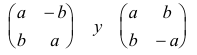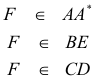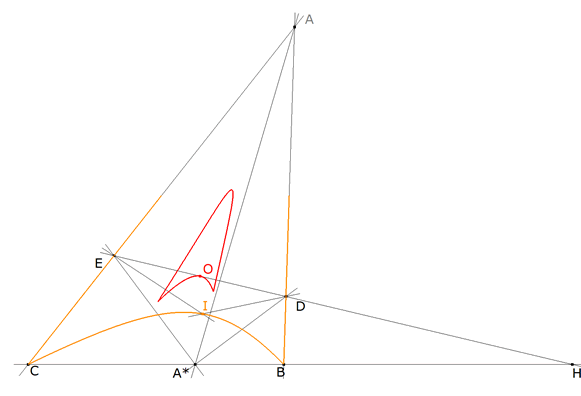Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 277

[1] Sea A* un punto interior de BC en el triángulo ABC. Las bisectrices interiores de loa ángulos BA*A y CA*A intersecan a AB y a AC en D y E respectivamente. Demostrar que AA*, BE y CD son concurrentes.

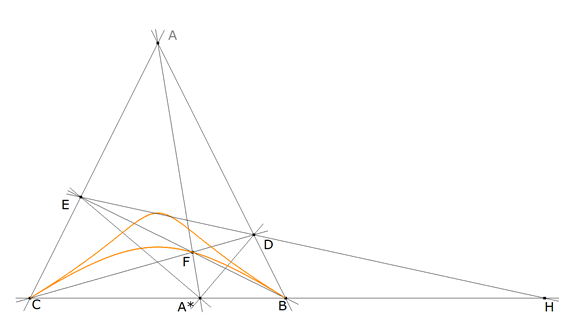
[2] Por Loeffer: Lugar geométrico del punto de concurrencia si ABC es equilátero.

[3] Por J.B. Romero : Lugar geométrico de los baricentros, circuncentros, ortocentros e incentros de los triángulos A*ED, rectángulos en A* cuando A* varia sobre BC

Romero, J.B. (2005): Comunicación personal. (Publicado en su versión original en Crux Mathematicorum, problema 2840, y en http://www.math.fau.edu/yiu/RecreationalMathematics.pdf (pág300-925), de Paul Yiu, Verano de 2003)

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de octubre de 2005)

INTRODUCCION

Sean r,r’,s,s’ cuatro rectas de un haz A*. En geometría clásica se dice que las rectas s, s’ son bisectrices de las rectas r, r’ si s y s’ son ejes ortogonales de simetría que transforman r en r’.

Si traducimos lo anterior al lenguaje proyectivo y usamos en los necesario el cuerpo C de los complejos, podemos obtener una vía para responder al enunciado.

- Empezaremos por el SEGUNDO TEOREMA de DESARGUES y de él deduciremos el TEOREMA UNO que nos permite hallar rectas y puntos conjugados armónicos por medio de un cuadrivértice.

- Identificamos homografías elípticas de rectas proyectivas reales con SEMEJANZAS DIRECTAS.

- Introducimos, a continuación, la ortogonalidad por medio de la INVOLUCIÓN CANÓNICA y de sus puntos fijos los PUNTOS CICLICOS.

- Caracterizamos las SEMEJANZAS como homografías cuya restricción a la recta de infinito conmuta con la INVOLUCIÓN CANÓNICA.

- A partir de aquí podemos definir ÁNGULO DE DOS RECTAS por medios proyectivos y a su vez concluir con la definición proyectiva de BISECTRICES.

- Acabamos redactando la SOLUCIÓN.

RECURSOS TEORICOS

SEGUNDO TEOREMA DE DESARGUES (Sin demostración)

figura 1

Sea un cuadrivértice y una recta que nos pasa por ninguno de los vértices del mismo. Entonces los lados opuestos del cuadrivértice cortan a la recta en puntos que se corresponden en una misma involución.

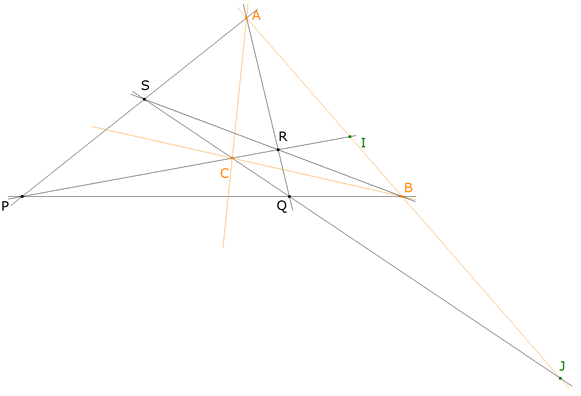
TEOREMA UNO

Dos lados del triángulo diagonal de un cuadrivértice son conjugados respecto los lados que pasan por el vértice diagonal correspondiente.

figura 2

DEMOSTRACIÓN UNO

Sea el cuadrivértice PQRS. Sean los vértices diagonales

Sean las rectas

Estas rectas cortan al lado AB en

Los puntos A y B son fijos en la involución que sobre AB se define por el SEGUNDO TEOREMA DE DESARGUES e I, J son homólogos en esta involución

c.q.d.

HOMOGRAFÍAS ELÍPTICAS DE UNA RECTA PROYECTIVA REAL Y LA SEMEJANZA DIRECTA

Una homografía

sin puntos fijos es inducida por un isomorfismo

que no admite ningún vector propio real. No obstante, en el campo complejo

Lo anterior nos demuestra que pasamos de una recta M a otra M’ = α(M) por medio de una semejanza directa.

La homografía α es una involución si y sólo si el ángulo de la semejanza es recto. Es decir, su matriz es

ORTOGONALIDAD (En el plano proyectivo real)

Para demostrar que dos rectas r y s, de vectores directores u y v respectivamente, son ortogonales, se utilizan principalmente dos métodos

Probar que el producto escalar u·v es nulo.

Encontrar una semejanza de ángulo ½π que lleva al vector u sobre el vector v.

Adoptamos el segundo método. Por el párrafo anterior sabemos que la matriz de esa semejanza es

Como los vectores directores de las rectas son sus direcciones, nos definen también sus puntos de infinito U y V respectivamente que en el plano proyectivo real serán (R es el cuerpo de los reales)

Pero hemos visto en el párrafo anterior que esta semejanza que define la ortogonalidad de u y v es un isomorfismo que induce una involución elíptica σ que transforma U en σ(U) = V, es decir es una involución elíptica de la recta del infinito.

Por lo tanto, podemos decir que dos rectas r y s son ortogonales si y sólo si σ intercambia los puntos de infinito de esas rectas U y V.

Recíprocamente, según el apartado anterior, el dar una involución elíptica σ de la recta del infinito pone de manifiesto una base que define la ortogonalidad que expresamos del siguiente modo

En la práctica, definiremos la ortogonalidad en un plano afín (inmerso en un plano proyectivo) mediante la elección de una involución de la recta del infinito. Esta involución se denomina INVOLUCIÓN CANÓNICA.

Si consideramos la recta del infinito y el cuerpo C de los complejos, la involución canónica σ tiene dos puntos fijos I y J y por lo tanto como

y de aquí al ser puntos distintos

con lo que concluimos que

Como los vectores propios de una semejanza de ángulo ½π son(1,i) y (1,-i) las coordenadas homogéneas de I y de J (puntos fijos) son

Los puntos fijos I, J de la involución canónica se denominan PUNTOS CICLICOS del plano porque toda cónica real del plano proyectivo que pasa por ellos es un círculo (pero eso es otra historia).

CARACTERZACION DE LAS SEMEJANZAS

Sea α una homografía plana que deja invariante el plano excluyendole la recta de infinito (carta afín). α restringida a esa carta afín es una semejanza si la restricción de α a la recta del infinito conmuta con la involución canónica.

DEMOSTRACION

Sea la homografía α de matriz

La restrcción de α y σ conmutan si y sólo si

igualdad que conduce a matrices de la forma

que representan respectivamente las semejanza directas e indirectas de la carta afín.

ÁNGULO DE DOS RECTAS.

Como el grupo de las semejanzas directas es isomorfo al grupo de los ángulos entre dos rectas podemos definir

Dos pares de rectas r, r’ y s, s’ forman el mismo ángulo si existe una homografía de la recta del infinito que conmute con la involución canónica y que transforme los puntos del infinito de r y s en los de r’ y s’.

BISECTRICES

Recordando que

Estamos en disposición de escribir su equivalente proyectivo

Se dice que las rectas s y s’ son bisectrices de las rectas, de su mismo haz, r y r’ si las rectas s y s’ son ortogonales y conjugadas respecto a r y r’

SOLUCIÓN

[1] CONSTRUIMOS EL ENUNCIADO (teniendo en cuenta la figura 2)

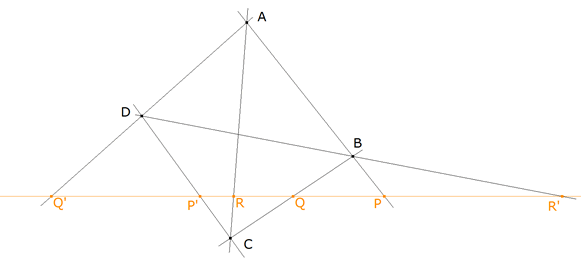
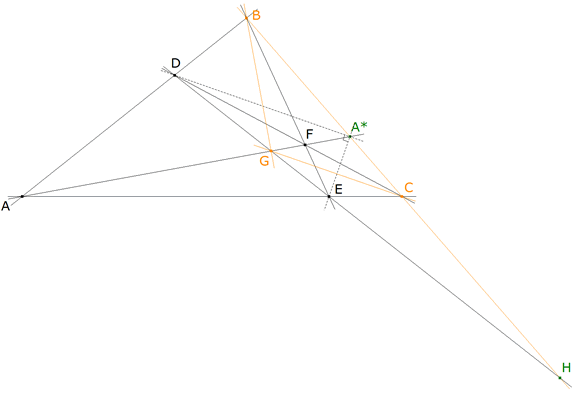
figura 3

Como A*D y A*E se definen como bisectrices de A*B y A*A son ortogonales y conjugadas; partiendo del haz A* podemos escribir

y proyectando ahora, con centro A, la recta DE sobre la recta BC, tenemos

vemos pues que A* y H (intersección de DE y BC) son conjugados armónicos respecto C y B y por lo tanto, recordando el TEOREMA UNO y la figura 2

Como H es el conjugado armónico de A* con respecto a B y C; siendo G = AA* ∩ DE podemos considerar que BCG es el triángulo diagonal del cuadrivértice ADFE siendo

POR LO TANTO AA*, BE Y CD CONCURREN

c.q.d.

[2]

figura 4

Recordemos que el enunciado dice que A* es interior a BC. El lugar geométrico sería sólo la rama inferior.

Si la curva fuera una cónica BF y CF serían rectas homográficas ( CHASLES STEINER); pero no lo son porque A* es variable.

Este lugar es una cuártica parecida al bicuerno simétrica respecto a la altura por A del triángulo equilátero que pasa por B y C,

[3]

figura 5

Para el lugar del ortocentro, basta darse cuenta que en un triángulo rectángulo el ortocentro es el vértice opuesto a la hipotenusa. El lugar del ortocentro es la recta BC

El incentro viene definido por la intersección de las bisectrices de los ángulos A*DE y A*ED. De nuevo como en el caso [3] el lugar no puede ser una cónica. El lugar es una cuártica por B y C. (En naranja en la figura 5)

Como el triángulo es rectángulo el lugar del circuncentro es el lugar del punto medio de DE y por tanto de nuevo obtendremos una cuártica. (En rojo en la figura 5)