Problema 277[1] Sea A* un punto interior de BC en el triángulo ABC.

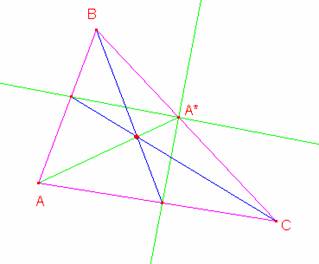
Las bisectrices interiores de loa ángulos BA*A y CA*A intersecan a AB y a AC en D y E respectivamente.

Demostrar que AA*, BE y CD son concurrentes.

Hasta aquí lo publicado en Crux y en Yiu.

Solución de William Rodríguez Chamache, Proyecto geometría interactiva (Perú)

De acuerdo a nuestra gráfica para que los segmentos AA*, BE y CD sean concurrentes se debe de cumplir que el producto de los segmentos AD.BA*.CE=BD:CA*AE

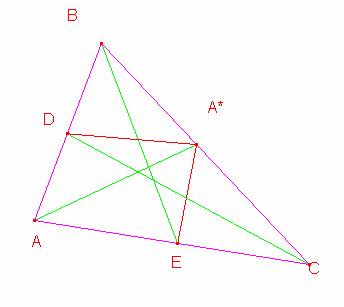
Como A*E es bisectriz del ángulo AA*E se cumple que:

AE=a , EC=b entonces AA*=ak y A*C=bk

Además como A*D es bisectriz de BA*A en el triángulo BA*A se cumple.

Si: BA*=c y AA*=ak entonces BD=cm y AD=akm

Finalmente observamos que la relación AD.BA*.CE=BD:CA*AE si cumple por lo tanto los segmentos AA*, BE y CD son concurrentes