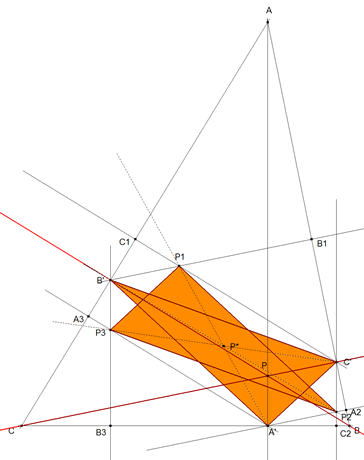
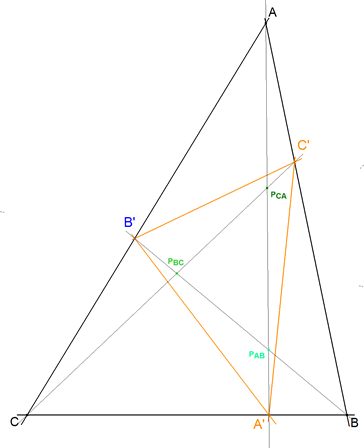
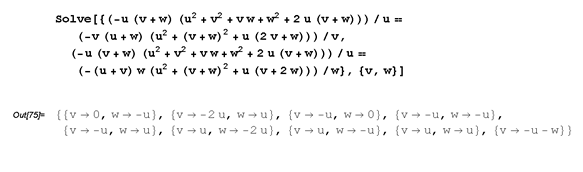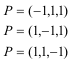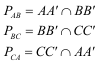De investigación

Problema 279

Sea ABC un triángulo y P un punto arbitrario en su plano donde se cortan las cevianas AA´, BB´y CC´, donde A´está en BC, B´ en CA y C´ en AB.

Definimos los siguientes pares de puntos : B1C1; A2C2; A3B3; tales que B1,A2 están en AB, C2,B3 están en BC, A3,C1 están en CA, y verificando que B´B1 //CC´, C´C1//BB´, A´A2//CC´, C´C2//AA´, A´A3//BB´, y B´B3//AA´

Definimos los puntos

P1 intersección de las rectas B´B1 y C´C1,

P2 intersección de las rectas A´A2 y C´C2,

P3 intersección de las rectas A´A3 y B'B3.

P* como intersección de las tres rectas A´P1, B´P2 y C´P3, que le podemos llamar como el punto conjugado de P respecto al triángulo ABC.

Demostrar que :

a) El triángulo P1P2P3 es semejante al triángulo A´B´C´, indicando las características de la transformación geométrica que lo produce.

b) Probar que el punto P* es el baricentro de cada uno de los pares de puntos P1, A´ , P2, B´, P3C´, respectivamente.

c) ¿Qué pasaría con el enunciado anterior y sus conclusiones (a), (b), si P fuera un punto notable del triángulo, baricentro, G, circuncentro, O, incentro, I, u ortocentro H.

d) Hallar todos los puntos del plano del triángulo ABC, tales que P= P*.

e) Hallar en cada uno de los casos el lugar geométrico de los puntos del plano del triángulo tales que :

e1) El triángulo A´B´C´ sea semejante al triángulo ABC,

e2) Los triángulos AC´B´, BA´C´, y CB´A´ sean semejantes al triangulo ABC,

e3) Los tres triángulos anteriores junto con A´B´C´ sean semejantes al triángulo ABC.

Romero, J. B. (2005): Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de noviembre de 2005)

SOLUCIÓN

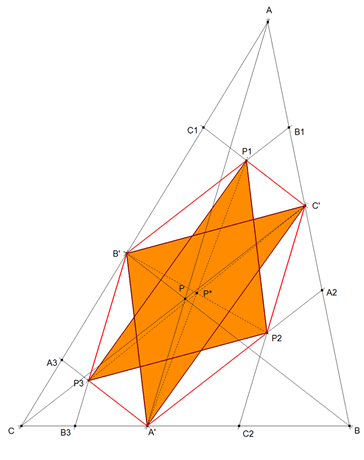
APARTADO (a)

figura 1

Los lados homólogos de los triángulos son paralelos, lo que equivale a decir que se cortan en la recta del infinito, aplicando el TEOREMA DE DESARGUES deducimos que las rectas que unen vértices homólogos son concurrentes en P*. Al ser el eje de homología la recta de infinito, la homología es una homotecia y de razón -1; porque los lados homólogos son paralelas entre paralelas y por tanto iguales. Esta transformación también puede verse como un giro de ángulo π con centro en P*. (Si observamos el exágono rojo de la figura, también podríamos haber usado el TEOREMA DE PASCAL y el DE BRIANCHON)

APARTADO (b)

El propio apartado (a) nos da la respuesta; como los pares de puntos dados son los homólogos en la transformación anterior, equidistan de P* y por tanto P* es su punto medio. Por ejemplo:

APARTADO (c)

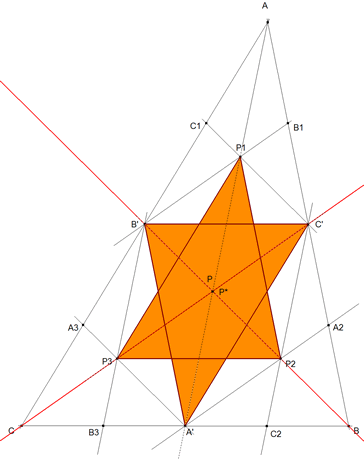
figura 2

c - baricentro G

En ese caso A’, B’ y C’ son los puntos medios de los lados BC, CA y AB y por tanto A’B’C’ es homotético de ABC con centro en G y razón -½; y por tanto, P1P2P3 es homotético de ABC con centro en P y razon +½.

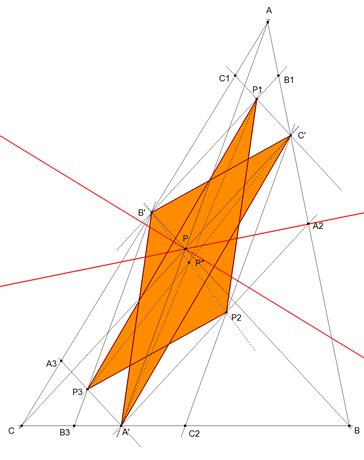
figura 3

c - circuncentro

Se conserva la misma transformación que en el caso (a). En esta ocasión, yo no distingo ninguna característica especial.

figura 4

c - incentro

Se conserva la misma transformación que en el caso (a). En esta ocasión, las cevianas son las bisectrices.

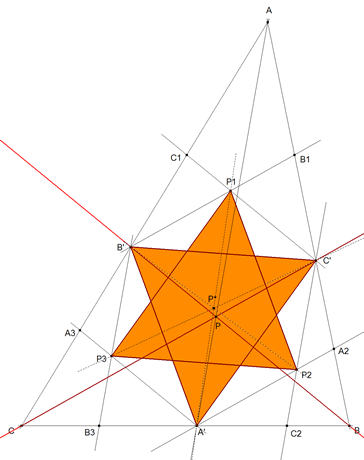
figura 5

c- ortocentro

Se conserva la misma transformación que en el caso (a). En esta ocasión, A’B’C’ es el triángulo órtico de ABC.

APARTADO (d)

Aprovechando ahora el trabajo realizado en baricéntricas por FRANCISCO JAVIER GARCÍA CAPITÁN

figura 6

Podemos pasar a buscar P* a partir de P

245.1_page_1.gif

figura 7

Si P coincide con P*, sus coordenadas son proporcionales y de aquí

245.1_page_2.gif

figura 8

d - primera y tercera solución

Si P recorre un lado del triángulo P*, recorre ese lado del triángulo. P y P* coincidirán en el punto medio de los lados.

d - segunda y sexta solución

Si P recorre una mediana del triángulo, P* recorre esa mediana del triángulo. P y P* coincidirán cuando se encuentren sobre dos medianas a la vez; es decir, cuando P sea el baricentro como se vio en el apartado C. Veamos más puntos sobre las medianas en el siguiente párrafo.

d - cuarta, quinta y séptima solución

Es decir son los puntos

que son los simétricos de cada vértice respecto el punto medio del lado opuesto. Estos puntos también están sobre las medianas.

d - octava solución

Que es el baricentro como ya sabíamos.

d - novena solución

Es la recta de infinito.

APARTADO (e)

subapartados e1 y e3

Se supone que se sabe resolver el siguiente problema:

“ En un triángulo dado, inscribir otro triángulo que sea semejante a un triángulo dado y que tenga uno de sus vértices en un punto dado de un lado del primero.”

Julius Petersen. Problema 352

figura 9

Tomamos un punto cualquiera B’ sobre CA. Con un vértice en B’ dibujamos un triángulo cualquiera semejante a ABC. Por ejemplo fijamos por B’ una recta vertical y por su intersección con BC trazamos una recta que forme con la anterior un ángulo igual a BAC; y por B’ otra recta que forme con la vertical inicial un ángulo ABC. Obtenemos el triángulo azul.

Con centro en B’ lo vamos girando hasta dejar el triángulo inscrito en ABC. Para ello, trazamos por el último vértice (azul) hallado una perpendicular al último lado (azul) hallado. Esta perpendicular corta AB en C’. Conocidos los ángulo hallamos A’ sobre BC a partir de B’C’.

figura 10

Determinado un triángulo cualquiera A’B’C’ semejante a ABC, hallamos las intersecciones de AA’, BB’ y CC’. Como en general no son cevianas no obtendremos un punto único; obtenemos tres puntos distintos

Hallaremos ahora el lugar geométrico de P_BC cuando B’ recorre CA. Es claro que BB’ y CC’ son rectas homográficas de una homografía entre B* y C* y por lo tanto (TEOREMA DE CHASLES STEINER) el lugar geométrico de P_BC es una cónica que pasa por B, C, P_BC y dos puntos más que podemos hallar como hemos hallado P_BC. Del mismo modo procedemos con P_AB y P_CA.

Resumiendo

El lugar de P_AB cuando B’ recorre CA es una cónica por A, B, P_AB ...

El lugar de P_BC cuando B’ recorre CA es una cónica por B, C, P_BC ...

El lugar de P_CA cuando B’ recorre CA es una cónica por C, A, P_CA ...

figura 11

Estas tres cónicas (elipses en este caso) coinciden en un único punto. Este punto de coincidencia ÚNICO es el BARICENTRO como ya habíamos visto.

En ese caso A’, B’ y C’ son los puntos medios de sus lados respectivos y por tanto AB’C’, BC’A’ y CA’B’ son semejantes a ABC. Vemos pues que este caso también resuelve la cuestión [subapartado (e3)].

subapartados e2

Supongamos que construimos la solución usando la igualdad de ángulos.

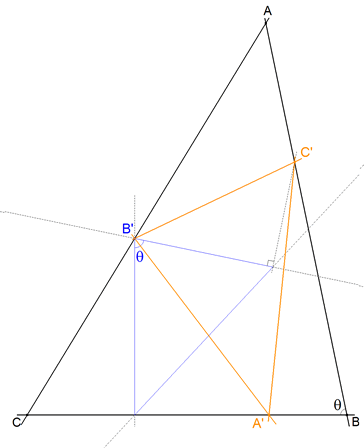
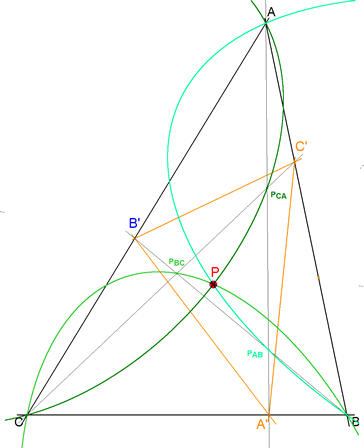
figura 12

Tomamos un punto B’ cualquiera sobre CA. Por B’ trazamos una recta que forme con CA un ángulo igual a B. Esta recta corta a AB en C’.

Por C’ trazamos una recta que forma con AB un ángulo igual a C. Esta recta corta a BC en A’.

B’C’ y A’C’ forman el mismo ángulo con AB y por lo tanto la perpendicular a AB por C’ es su bisectriz. Podemos usar el mismo razonamiento para los otros puntos A’ y C’.

Resumiendo. Para que los triángulos mencionados sean semejantes a ABC, debe ser:

C’A’ y A’B’ tendrán por bisectriz a la perpendicular a BC por A’

A’B’ y B’C’ tendrán por bisectriz a la perpendicular a CA por B’

B’C? y C’A’ tendrán por bisectriz a la perpendicular a AB por C’

Pero esto, como hemos visto varias veces en estas páginas de RICARDO BARROSO, sólo ocurre cuando A’B’C’ es el triángulo órtico de ABC.