De investigación: Propuesto por José Carlos Chávez Sandoval, estudiante peruano de Matemática Pura en la Universidad Nacional Mayor de San Marcos Problema 280 -Teorema de Seydewitz.
Si un triángulo se inscribe en una circunferencia, cualquier recta conjugada con respecto a uno de sus lados corta a los otros dos en puntos conjugados. (El teorema se refiere a una cónica general). Coxeter, H.S.M. (1971): Fundamentos de Geometría. Limusa-Wiley. SA (México) (pag. 290) Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de noviembre de 2005) |
|
|
|
1. INTRODUCCION |
|
|
|
Resolvemos el caso para una cónica Γ cualquiera. Usaremos que una recta es conjugada de otra, respecto una cónica dada, si la primera es polar de un punto de la segunda. Polo (polar) Estos conceptos se introducen viendo algunas propiedades de cuerdas de la cónica. El concepto de POLO lo vemos en el teorema 2.5 e identificamos la recta POLAR. Lo vemos examinando primero tres teoremas auxiliares: |
|
teorema 2.1 |
Recíproco de la definición de proyección entre haces de rectas. Util para determinar alineaciones. |
teorema 2.2 |
SEGUNDO TEOREMA DE DESARGUES demostrado en el problema 183 de las páginas de RICARDO BARROSO |
teorema 2.3 |
Con el teorema 2.2 establecemos las propiedades armónicas de las diagonales del cuadrilátero. |
Vistos los conceptos de POLO (y POLAR), introducimos un método para determinar la polar de un punto respecto a una cónica; a partir de este método construimos la solución a nuestro problema ayudados por el: |
|
teorema 2.4
|
SEGUNDO TEOREMA DE DESARGUES EXTENDIDO A LAS CÓNICAS. |
|
|
2. POLOS |
|
|
|
Teorema 2.1 Cuando dos haces de cuatro rectas que se corresponden una a una, respectivamente, tienen sus razones dobles iguales (son homográficas), si una de las rectas coincide con su imagen, las tres rectas restantes del haz cortan a sus rectas correspondientes en el otro haz en tres puntos situados en línea recta. (El teorema recíproco no es más que la definición de una proyección entre haces de rectas.)
|
|
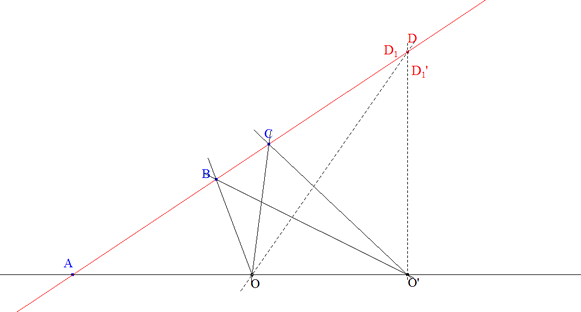
Demostración 2.1 Sean O* y O’* los dos haces. Sean OA, OB, OC, OD (figura 1)las cuatro rectas de O* y O’A, O’B, O’C, O’D las cuatro rectas de O’* que les corresponden respectivamente. Supongamos que las rectas que coinciden son OA y O’A; entonces mostraremos que los puntos de intersección de cada recta con su correspondiente, B=OB∩O’B, C=OC∩O’C, D=OD∩O’D, están en línea recta. Sean A=BC∩OO’, D1=BC∩OD y D1'=BC∩OD’. Como los dos haces son homográficos, conservan la razón doble; tenemos [OA,OB,OC,OD1]=[O’A,O’B,O’C,OD1'] y por lo tanto D1=D1' con lo que OD y O’D se cortan en BC. |
|
|
|
Teorema 2.2 Segundo Teorema de Desargues,(Ver problema 183): Sea un cuadrángulo ABCD y sea r una recta que no pasa por ninguno de sus vértices. Los lados opuestos del cuadrángulo cortan a r en puntos que se corresponden en una misma involución. |
|
|
|
Teorema 2.3 En todo cuadrilátero, las dos diagonales dividen armónicamente la recta que une los puntos de encuentro de los lados opuestos. Demostración 2.3 Es consecuencia del segundo teorema de Desargues; basta con tomar como transversal r la recta que une los puntos de encuentro de los lados opuestos; cada uno de esos puntos será un punto doble de la involución; además en una involución σ de puntos doble A y B, la razón doble cumple, para todo punto P, (A, B, P, σ(P)) = -1, que al fin y al cabo es la condición de que P y σ(P)sean conjugados armónicos. |
|
|
|
Teorema 2.4 - Extensión del Segundo Teorema de Desargues (Cónicas): Cuando un cuadrilátero está inscrito a una cónica, una transversal cualquiera r encuentra a los dos pares de lados opuestos y a la cónica en tres pares de puntos homólogos en una involución de la recta r.
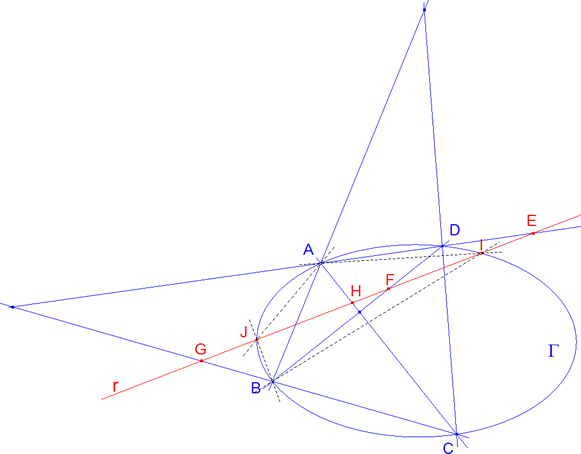
Demostración 2.4 Sean ABCD los vértices del cuadrilátero y r la recta que corta a los lados AD, BD, BC, AC respectivamente en E, F, G, H y a la cónica en I y J. Tenemos entonces la siguiente igualdad de razones dobles [AD,AC,AI,AJ]=[BD,BC,BI,BJ] AD, AC, AI, AJ cortan a r en E, H,I, J BD, BC, BI, BJ cortan a r en F, G,I, J se cumple entonces [E,H,I,J]=[F,G,I,J]=[G,F,J,I] la última igualdad es gracias a las propiedades de la razón doble. Deducimos entonces que I, J son puntos homólogos de la involución que intercambia E con H y G con F. Esta involución es la definida por el cuadrilátero en la recta r (SEGUNDO TEOREMA DE DESARGUES). |
|
|
|
Después de estos cuatro primeros teoremas ya tenemos lo necesario para atacar la definición de POLAR de un punto. |
|
|
|
Teorema 2.5 (polar de un punto) Cuando varias cuerdas de una cónica pasan por un mismo punto: primero Los puntos de encuentro de las rectas que unen dos a dos los extremos de dos cuerdas cualesquiera están sobre una misma recta. segundo Las tangentes a los extremos de cada cuerda se cortan sobre esta recta. tercero Esta recta es el lugar de los puntos conjugados armónicos del punto de encuentro de las cuerdas con respecto a los extremos de cada cuerda.
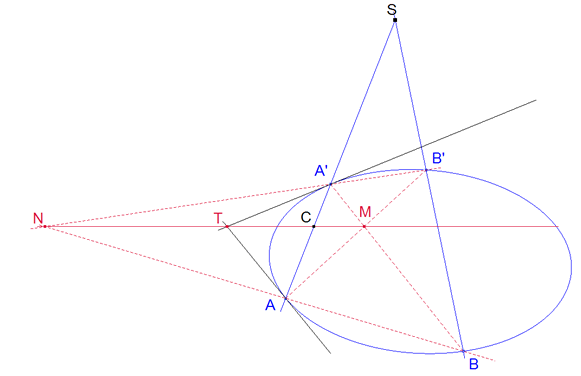
Demostración 2.5 Sean AA’, BB’ dos cuerdas y S su punto de encuentro (figura 3). Probemos primero que los puntos M, N intersección de las rectas que unen los extremos de estas dos cuerdas y el punto T de encuentro de las tangentes por los extremos A, A’, de una de las cuerdas, son tres puntos en línea recta. Como son puntos y tangentes de la misma cónica, el haz de rectas AT, AB, AB’, AA’ es homográfico al haz A’A, A’B, A’B’, A’T lo cual supone la igualdad de razones dobles [AT,A B,AB’,AA’]=[A’A,A’B,A’B’,A’T]=[A’T,A’B’,A’B.A’A], vemos que AA’ coincide con su imagen A’A, según el teorema 2.1 los puntos T=AT∩A’T, N=AB∩A’B’, M=AB’∩A’B están alineados. Teniendo ahora en cuenta el teorema 2.3, para el cuadrilátero AMA’N, la intersección de las diagonales C=AA’∩MN es el conjugado armónico con respecto a los vértices A y A’ del punto S en el que la recta, que une los puntos de encuentro de los lados opuestos del cuadrilátero B,B’, encuentra a la diagonal AA’. La recta MN se determina por medio de una sola cuerda AA’, ya que pasa por T punto de encuentro de las tangentes por A y A’ y por C, conjugado armónico de S respecto a A y A’. La recta MN es la POLAR del punto S y éste es el POLO de la recta. Las rectas desde el polo a un punto de encuentro de la polar con la cónica es la tangente a la cónica en ese punto; si no fuera tangente, tendría otro punto diferente de encuentro con la cónica y el conjugado armónico de S respecto a estos dos puntos no sería el supuesto. |
|
|
|
3. SOLUCION |
|
|
|
Del teorema 2.5 deducimos un método sencillo para obtener la polar de un punto respecto a una cónica.
Uniendo dos a dos los puntos los puntos de encuentro de las transversales y la cónica por medio de rectas; los puntos de encuentro de estas rectas están en la polar. |
|
|
|
Pero en esta construcción podemos identificar nuestro enunciado:
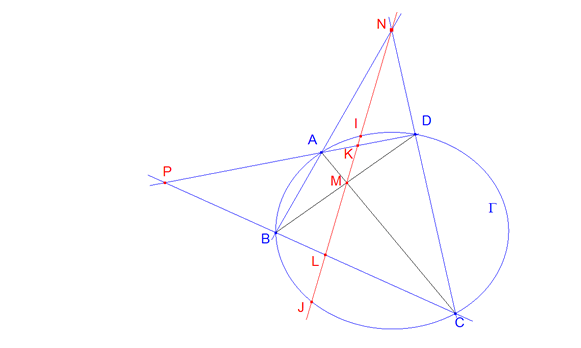
Identificamos, por ejemplo, el triángulo ABC inscrito en la cónica Γ.
Un punto P pertenece a BC. MN es la polar de P. MN es la conjugada del lado BC.
MN corta a AB en N y a AC en M.
MN corta al cuadrilátero; pero pasa por dos de sus vértices. Como corta a los lados opuestos AB y CD en el mismo punto N; N es un punto doble de la involución (segundo teorema de Desargues) inducida en MN por el cuadrilátero. El mismo razonamiento podemos hacer con el punto M.
Pero por el segundo teorema de Desargues extendido a las cónicas, I, J se intercambian en la involución que identifica el teorema. Sea σ esa involución; podemos escribir las siguientes razones dobles: [M,N,I,J]=[σ(M),σ(N),σ(I),σ(J)]=[M,N,J,I]=1/[M,N,I,J]
de lo que se deduce [M,N,I,J]2=1
Pero como todos los puntos son distintos la razón doble no puede ser 1 y podemos escribir [M,N,I,J]=-1
Que expresa que M y N son conjugados respecto de I,J; pero I,J están sobre la cónica Γ lo que concluye el resultado pedido por el enunciado. |
|