Problema 281

11.20 Les hipotenuses de dos triangles rectangles semblants estan sobre dues rectes m, m’ que formen un angle de 30º i es tallen en un punt P. Els vèrtexs B, C del primer disten de P, PB=1, PC=6, i els vèrtexs B’, C’ del segon, homòlegs de B i C en la semblança, PB’=2, PC’=4,5. Els catets del primer triangle mesuren b=4 c=3. Sabent que la semblança entre els dos triangles és directa, Determineu:

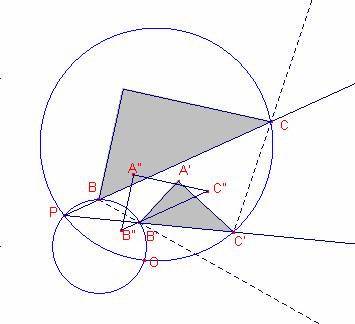
a) el centre o punt doble de la semblança directa.

b) dibuixat el primer triangle ABC, Determineu A’, homòleg del vèrtex A de l’angle recte del primer, utilitzant el gir i la homotècia del producte de la qual resulta la semblança.

Solució:

La raó de semblança dels triangles , és 2:1

Volem construir un triangle igual al triangle sobre la recta m (recta que passa per B, C)

Aleshores els triangles , serien homòlegs.

Aleshores els triangles , es transformarien amb en un gir de 30º i amb el mateix centre que el centre que el centre d’homotècia.

Construïm l’arc capaç de 30º del segment BB’ i l’arc capaç de 30º del segment CC’

La intersecció dels dos arc en donaria en centre del gir.

Dibuixem el triangle de catets , .

L’homòleg A” del vèrtex A és el punt mig del segment (perquè la raó de semblança és 2).

L’homòleg B” del vèrtex B és el punt mig del segment

L’homòlèg C” del vèrtex C és el punt mig del segment

A’ és la rotació de -30º del punt A” amb centre O.

Construcció Amb Cabri:

Figura barroso281.fig

Applet created on 16/11/05 by Ricard Peiró with CabriJava