Problema 281

11.20 Las hipotenusas de dos triángulos rectángulos semejantes están sobre dos rectas m y m’ que forman un ángulo de 30º y se cortan en un punto P. Los vértices B y C del primero distan de P, PB=1, PC=6, y los vértices B’y C’ del segundo, homólogos de B y C en la semejanza, PB’=2 PC’=4,5. Los catetos del primer triángulo miden b=4 c=3. Sabiendo que la semejanza entre los dos triángulos es directa, halla:

a) el centro o punto doble de la semejanza directa.

b) dibujado el primer triángulo ABC, halla A’, homólogo del vértice A del ángulo recto del primero, utilizando para ello el giro y la homotecia de cuyo producto resulta la semejanza.

Martínez, J. Bujanda, M.P., Velloso, J.M. (1984): Matemáticas -1 (Escuelas Universitarias de Magisterio de E.G.B.) Ediciones S.M. Madrid (pag 382).

La razón de semejanza de los triángulos , es 2:1

Queremos construir un triángulo igual al triángulo

Entonces los triángulos , serien homólogos.

Los triángulos , se transformarían con en un giro de 30º i con el mismo centro que el centro de homotecia.

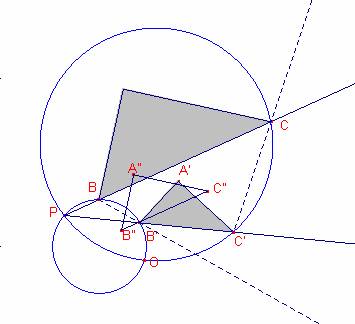
Construimos el arco capaz de 30º del segmento BB’ y el arco capaz de 30º del segmento CC’

La intersección de los dos arcos nos donaría en centro del giro.

Dibujemos el triángulo de catetos , .

El homólogo A” del vértice A es el punto medio del segmento (porque la razón de semejanza es 2).

L’homólogo B” del vértice B es el punto medio del segmento

L’homólogo C” del vértice C es el punto medio del segmento

A’ es la rotación de -30º del punto A” con centro O.

Construcción con Cabri:

Figura barroso281.fig

Applet created on 16/11/05 by Ricard Peiró with CabriJava