Para el aula

Problema 281

11.20 Las hipotenusas de dos triángulos rectángulos semejantes están sobre dos rectas m y m’ que forman un ángulo de 30º y se cortan en un punto P. Los vértices B y C del primero distan de P, PB=1, PC=6, y los vértices B’y C’ del segundo, homólogos de B y C en la semejanza, PB’=2 PC’=4,5. Los catetos del primer triángulo miden b=4 c=3. Sabiendo que la semejanza entre los dos triángulos es directa, halla:

a) el centro o punto doble de la semejanza directa.

b) dibujado el primer triángulo ABC, halla A’, homólogo del vértice A del ángulo recto del primero, utilizando para ello el giro y la homotecia de cuyo producto resulta la semejanza.

Martínez, J. Bujanda, M.P., Velloso, J.M. (1984): Matemáticas -1 (Escuelas Universitarias de Magisterio de E.G.B.) Ediciones S.M. Madrid (Pág. 382).

Con el permiso de Mari Paz Bujanda, a quien el director agradece su gentileza.

Solución Saturnino Campo Ruiz, profesor del IES Fray Luis de León de Salamanca.-

a) El centro de semejanza O es el único punto fijo en la transformación. Los triángulos OCB y OC’B’ son semejantes. Si P es la intersección de BC con B’C’, B y B’ están en el arco capaz de OP y ángulo f = áng(OBC)=áng(OB’C’). Del mismo modo con el ángulo d = áng(OCP) = áng(OC’P) encontramos que O, P, C y C’ son concíclicos. En resumen: O se obtiene como intersección de dos circunferencias según se puede observar en la figura.

Aplicando estas ideas al caso particular que nos ocupa y calculamos en centro O de semejanza. ( El punto B’ no está sobre el lado AB ni tampoco A sobre A’C’ como parece sugerir la figura). Hemos tomado la unidad de medida igual a 2,4 cm.

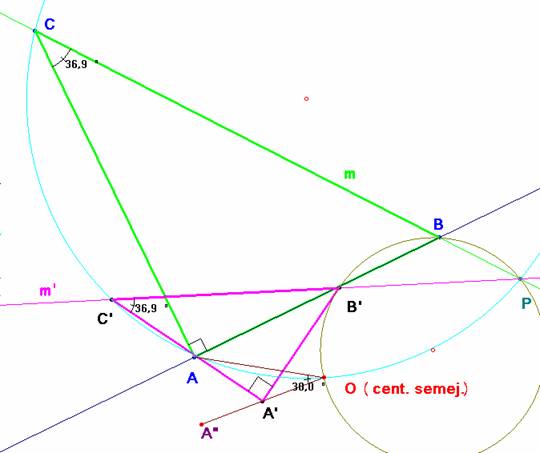
b) A partir de A, con centro en O realizamos un giro de 30º que nos lleva el punto A hasta A”. Como la homotecia tiene razón ½ para hallar A’ basta con tomar el punto medio del segmento OA”.