De investigación.
Problema 282.-

Si un triángulo equilátero está inscrito en una circunferencia, la suma de los cuadrados de los segmentos que unen cualquier punto de la circunferencia a los tres vértices del triángulo es constante.

Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid.
Brockway, G. E. (1895): American Mathematical Monthly, (Volumen II, May) p. 158.

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba, España.

Lema previo (Problema 125 )
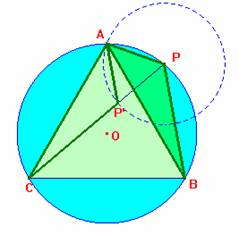
Sea P un punto del arco menor AB de la circunferencia circunscrita del triángulo equilátero ABC. Se tiene que, CP = AP + BP

Sol: El triángulo APP' es equilátero ya que el ángulo en P es igual al ángulo inscrito en la circunferencia <ABC= 60º y, por otra parte PP' = PA, por la construcción hecha en la figura adjunta.

De este modo, veamos ahora cómo los triángulos AP'C y APB son congruentes. Este hecho es cierto sin más que probar que tienen dos ángulos iguales y uno de los lados homólogos iguales entre sí.
Para ello, tenemos que:
<APB = 120º = <AP'C; y que <ABP = <ACP' y así el tercer ángulo <CAP' = <BAP.
Como AP=AP' (también AC = AB) entonces se tendrá que: CP' = BP, pero como CP' = CP - AP.

En definitiva, AP + BP = CP , c.q.d.

Teniendo en cuenta este resultado, el problema que nos ocupa se simplifica notablemente como veremos a continuación.
Si el triángulo equilátero ABC tiene por lado a, sean entonces las siguientes expresiones correspondientes a la aplicación del teorema del coseno para los triángulos APB, BPC y CPA.

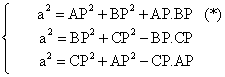
Sumando las tres igualdades obtenemos: 3∙a² =2∙(AP²+BP²+CP²) + AP∙BP −CP∙(BP+AP) (1)

Como quiera que CP = AP + BP, por el lema anterior, entonces (1) adquiere la siguiente expresión:

3∙a² =2∙(AP²+BP²+CP²) + AP∙BP −(BP+AP)² ;

3∙a² =2∙(AP²+BP²+CP²) − ( AP² + BP² + AP∙BP) ;

Pero la expresión AP² + BP² + AP∙BP = a² (*)

Luego en definitiva: 3∙a² =2∙(AP² + BP² + CP² ) − a²

De donde resulta: AP² + BP² + CP² = 2∙a²