De investigación.

Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 282

2) Si un triángulo equilátero está inscrito en una circunferencia, la suma de los cuadrados de los segmentos que unen cualquier punto de la circunferencia a los tres vértices del triángulo es constante.

Brockway, G. E. (1895): American Mathematical Monthly, (Volumen II, May) p. 158 

Demostración de Saturnino Campo Ruiz, profesor del IES Fray Luis de León de Salamanca.

 

 

Para el triángulo equilátero inscrito en la circunferencia se verifica

 

PC = PA + PB        (1)

 

(visto en otro problema de la revista), sin más que aplicar el teorema de Ptolomeo al cuadrilátero inscrito PACB. Según este teorema el producto de las diagonales es igual a la suma de los productos de los lados opuestos, por tanto:

 

PC·AB = PA·BC + PB·AC

 

Al ser AB=AC=BC, simplificando se obtiene la relación (1).

 

 

 

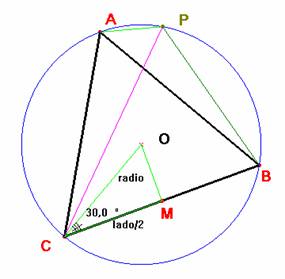
Aplicando al triángulo PAB el teorema del coseno, teniendo en cuenta que el ángulo PAB mide 120º, obtenemos:

 

(AB)2 = (PA)2  + (PB)2 - 2·PA·PB·cos120 = (PA)2  + (PB)2 + PA·PB       (2)

 

Para la suma de los cuadrados, aplicando primeramente (1)

 

 (PA)2  + (PB)2 + (PC)2 = (PA)2  + (PB)2 + (PA + PB)2=2((PA)2 + (PB)2 + PA·PB)

 

y después (2)

                        (PA)2  + (PB)2  + (PC)2  = 2·(AB)2 

 

Por tanto la suma de los cuadrados de las distancias desde P a los vértices del triángulo equilátero es igual al doble del cuadrado del lado de éste.

El lado del triángulo equilátero inscrito mide lado =AB =·r, donde r es el radio de la circunferencia circunscrita, como se deduce fácilmente de la observación del triángulo rectángulo OMC. El valor de la constante es  2·(AB)2 =2·(·r)2 = 6·r2.