Problema 284 de triánguloscabri
|
429. Construir un triángulo conociendo A, a,
w'a (w'a es la bisectriz exterior de A).
|
|
Sapiña, J. (1955): Problemas Gráficos
de Geometría,Litograf. Madrid. (Aparejador, Perito Industrial,
Profesor ) (p.65)
|
Solución de Juan Sapiña Borja, presentada por Francisco
Javier García Capitán
La solución que Juan Sapiña da a este problema es la siguiente:
Problema 429. Construir un
triángulo conociendo el ángulo A, el lado a
y la bisectriz exterior w'a del ángulo A.
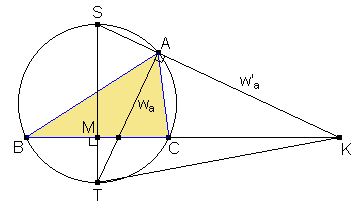 KA
corta en S a la circunferencia, por ser ÐTAK
= ÐTAS = 90º. Por ser TK
hipotenusa común a TAK y TMK, tenemos que TMAK
es inscriptible y se verifica que KA
corta en S a la circunferencia, por ser ÐTAK
= ÐTAS = 90º. Por ser TK
hipotenusa común a TAK y TMK, tenemos que TMAK
es inscriptible y se verifica que
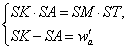
Esto permite calcular SK. Sobre BC trazamos
el arco capaz para el ángulo A. Trazamos una perpendicular
a BC por el punto medio M de AB y hallamos S.
Con radio SK fijamos K y al trazar KS obtenemos
A.
|
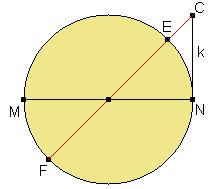 Construcción
previa. Sapiña usa la construcción de segmentos x e
y tales que
Construcción
previa. Sapiña usa la construcción de segmentos x e
y tales que
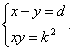
Según vemos en el libro de Bruño, para realizar
esta construcción, trazamos una circunferencia con diámetro MN
= d. Por el punto N trazamos una perpendicular NC = k
y unimos C con cel centro de la circunferencia hasta volver a cortarla
en F. Entonces tendremos CF = x y CE = y.
 Solución
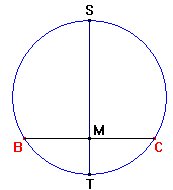
del problema. Nuestro primer paso para llevar a cabo la construcción
es fijar el segmento BC de longitud a y construir el arco capaz
de dicho segmento para el ángulo A.
Solución
del problema. Nuestro primer paso para llevar a cabo la construcción
es fijar el segmento BC de longitud a y construir el arco capaz
de dicho segmento para el ángulo A.
A continuación trazamos el diámetro ST perpendicular
a BC y el punto medio M de BC.
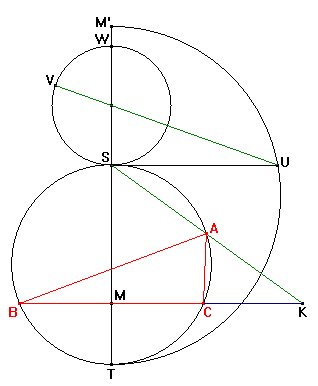 Ahora hallamos el punto M' simétrico de M respecto de S
y una semicircunferencia de diámetro M'T.
Ahora hallamos el punto M' simétrico de M respecto de S
y una semicircunferencia de diámetro M'T.
La perpendicular por S a TM' corta en U a
la semicircunferencia y SU es la media geométrica de SM'=SM
y ST.
Ahora podemos usar la construcción previa
con SU y w'a, de manera que marcamos en la recta TS un
punto W tal que SW = w'a, trazamos una circunferencia con diámetro
SW y unimos U con el centro de dicha circunferencia hasta cortar
otra vez a la misma en V. El segmento UV será igual a nuestra
distancia SK.
Finalmente, siguiendo en todo momento las indicaciones de Sapiña,
trazamos un arco con centro S y radio UV que determina el punto
K y unimos K con S para obtener A sobre el arco capaz.
Applet de CabriJava.
 KA
corta en S a la circunferencia, por ser ÐTAK
= ÐTAS = 90º. Por ser TK
hipotenusa común a TAK y TMK, tenemos que TMAK
es inscriptible y se verifica que
KA
corta en S a la circunferencia, por ser ÐTAK
= ÐTAS = 90º. Por ser TK
hipotenusa común a TAK y TMK, tenemos que TMAK
es inscriptible y se verifica que 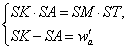

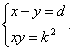
 Solución
del problema. Nuestro primer paso para llevar a cabo la construcción
es fijar el segmento BC de longitud a y construir el arco capaz
de dicho segmento para el ángulo A.
Solución
del problema. Nuestro primer paso para llevar a cabo la construcción
es fijar el segmento BC de longitud a y construir el arco capaz
de dicho segmento para el ángulo A.  Ahora hallamos el punto M' simétrico de M respecto de S
y una semicircunferencia de diámetro M'T.
Ahora hallamos el punto M' simétrico de M respecto de S
y una semicircunferencia de diámetro M'T.