Problema 285 de triánguloscabri

Sea la circunferencia circunscrita a un triángulo rectángulo en el vértice A. Consideremos una ceviana arbitraria AA', donde A' es su pie sobre el lado BC, y sea A*, el punto donde corta la circunferencia circunscrita. Por los vértices B y C, trazamos los segmentos BB* y CC*  paralelos a AA', y donde B* y C* son los puntos donde estos segmentos cortan a la circunferencia circunscrita, cuyo centro es O. Probar que:
a) El triángulo A*B*C*  es congruente o isométrico al triángulo ABC.
b) Si G y G* son los baricentros de los triángulos ABC y A*B*C*, entonces el segmento GG* es paralelo a AA*  y es 1/3 de AA*. ¿Qué ocurre con los incentros de esos triángulos con relación a AA'?
c) Al variar la ceviana AA' sobre el lado BC se construyen infinitos triángulos congruentes a ABC. Se pide
c1) Lugar geométrico descrito por  todos los baricentros de esos triángulos
c2) Lugar geométrico descrito por todos los incentros de esos triángulos.
d) ¿Qué se podría decir si hacemos la construcción anterior para los catetos del triángulo rectángulo anterior?
e) ¿Qué se podría decir de todo lo anterior para un triángulo cualquiera, obtusángulo o acutángulo?
Propuesto por Juan Bosco Romero Márquez

Solución de Francisco Javier García Capitán

a) El triángulo A*B*C*  es congruente o isométrico al triángulo ABC.

Podemos comprobar que este enunciado es cierto sin imponer que el triángulo ABC es rectángulo en A. En la figura de la derecha hemos llamado D y E a las intersecciones de AB, A*B* y AC, A*C* respectivamente, y podemos observar que

ÐB*A*A = ÐA*B*B (por ser AA* y BB* paralelas) = ÐBAA* (por ser ángulos inscritos que abarcan el mismo arco).

De la misma forma ÐC*A*A = ÐCAA*. Sumando ambas igualdades obtenemos que ÐA* = ÐA.

Además, al ser isósceles los triángulos BB*D y AA*D resulta que A*B*=AB, y de la misma forma A*C* = AC, por lo que los triángulo A*B*C, ABC tiene los ángulos ÐA* ,ÐA iguales y los lados comprendidos iguales, resultando entonces que los triángulos son congurentes, c.q.d.

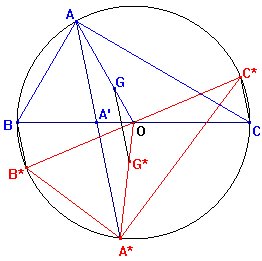b) Si G y G* son los baricentros de los triángulos ABC y A*B*C*, entonces el segmento GG* es paralelo a AA*  y es 1/3 de AA*. ¿Qué ocurre con los incentros de esos triángulos con relación a AA'?

Observemos que para cualquier triángulo ABC, sin necesidad de ser rectángulo, el triángulo A*B*C* es el simétrico de ABC respecto de la mediatriz de AA* (vemos que los acos AA* y BB*, medidos en sentido antihorario tienen el mismo punto medio).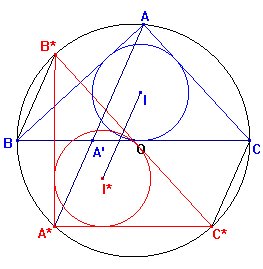

Entonces será también G* el simétrico de G y el segmento GG* será paralelo a AA*.

En el caso del triángulo rectángulo, tendremos además que OA y OA* son medianas y que OG:OA = OG*:OA* = 1/3. Por tanto GG*:AA* = 1:3.

Teniendo en cuenta que el triángulo A*B*C* es el simétrico de ABC respecto de la mediatriz de AA*, el incentro I* de A*B*C* es el simétrico del incentro I de ABC y así la recta II* es paralela a AA* y AA', y esto es cierto para cualquier triángulo ABC, sin necesidad de que ABC sea rectángulo.
c) Al variar la ceviana AA' sobre el lado BC se construyen infinitos triángulos congruentes a ABC. Se pide
c1) Lugar geométrico descrito por  todos los baricentros de esos triángulos
c2) Lugar geométrico descrito por todos los incentros de esos triángulos.

Hemos dicho que siempre el triángulo A*B*C* es el simétrico de ABC respecto de la mediatriz de AA* . El circuncentro O es común a todos los triángulos. Entonces:

c1) El lugar de G* será una circunferencia con centro O y radio OG.
c2) El lugar de I* será una circunferencia con centro O y radio OI.

En ambos casos el lugar geométrico será la circunferencia completa si permitimos a A' variar en toda la recta BC.
d) ¿Qué se podría decir si hacemos la construcción anterior para los catetos del triángulo rectángulo anterior?
e) ¿Qué se podría decir de todo lo anterior para un triángulo cualquiera, obtusángulo o acutángulo?

Ya hemos ido diciendo lo que ocurre en general en algunas de las cuestiones tratadas para el triángulo rectángulo. Repasemos y completemos:

a) El triángulo A*B*C*  es congruente o isométrico al triángulo ABC.

Esto siempre es cierto.

b) Si G y G* son los baricentros de los triángulos ABC y A*B*C*, entonces el segmento GG* es paralelo a AA*  y es 1/3 de AA*. ¿Qué ocurre con los incentros de esos triángulos con relación a AA'?

GG* siempre es paralelo a AA* pero no tiene por que ser 1/3 de AA*. Investiguemos esto: En un triángulo cualquiera, ¿para qué punto A' se produce GG* = (1/3) AA*? Para responder a esta pregunta usamos coordenadas baricéntricas:

 
  • Vemos que la expresión se anula cuando el triángulo es rectángulo en A y en ese caso la relación se cumple para cualquier A'.
  • El factor v+w se anula cuando A' es el punto del infinito de la recta BC, es decir cuando trazamos una paralela a BC por A y A* está en dicha paralela.
  • El último factor del denominador se anula cuando A' es el punto , que es el conjugado armónico de resepecto de B y C., el pie de la altura trazada por A. Comprobémoslo con Cabri:
    • Dado el triángulo ABC trazamos su altura AK y elegimos un punto P cualquiera de AB. La recta PK corta a la paralela a AB por C en L. Hallamos el simétrico L' de L respecto de C y trazamos la recta L'P, que corta a la recta BC en A', que será el conjugado armónico de K respecto de B y C.
    • Ahora hacemos la construcción partiendo de este A'. En el applet se puede mover el triángulo ABC y vemos esta construcción.


c) Al variar la ceviana AA' sobre el lado BC se construyen infinitos triángulos congruentes a ABC. Se pide
c1) Lugar geométrico descrito por  todos los baricentros de esos triángulos
c2) Lugar geométrico descrito por todos los incentros de esos triángulos.

Estas cuestiones ya han quedado respondidas en general.

c1) El lugar de G* será una circunferencia con centro O y radio OG.
c2) El lugar de I* será una circunferencia con centro O y radio OI.