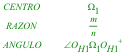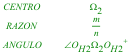En 1937, la Librairie de l’Enseignement Technique Léon Eyrolles en su colección

LES MATHÉMATIQUES

pour l’enseignement secondaire

publicó de los autores

G. ILIOVICI ET P. ROBERT

la siguiente obra

GÉOMÉTRIE

à l’usage des élèves de la classe de Mathématiques, des Candidats aux grandes Écoles (Saint-Cyr, Institut Agronomique, etc...) et des élèves des Écoles normales supérieures de l’Enseignement primaire.

Esta obra publicada en un solo volumen está dividida en dos partes, una parte de teoría y una parte de problemas. Cada parte está dividida en dos libros. El libro I que lleva por subtítulo TRANSFORMACIONES y el libro II que lleva por título CÓNICAS.

Los problemas están catalogados en tres tipos. Tipo A para los ejercicios elementales y fáciles, tipo B para aquellos cuya dificultad es más grandes, y tipo C para los problemas catalogados como los más difíciles. Algunos problemas están marcados con un asterisco (*), lo que significa que sólo son atacables después de haber trabajado toda la obra.

ILIOVICI y ROBERT, en la parte de PROBLEMAS del Libro I y para el capítulo IV, Homotecia y semejanza, proponen con el número 73 el siguiente enunciado que califican como tipo A:

Dados tres círculos de centros O, O’, O”, construir un triángulo semejante al triángulo OO’O” cuyos vértices estén, respectivamente, sobre los tres círculos dados.

Julius Petersen, en MÉTHODES ET THÉORIES POUR LA RÉSOLUTION DES PROBLÈMES DE CONSTRUCTIONS GÉOMÉTRIQUES. GAUTHIER-VILLARS. PARIS 1880, propone, con el número 382, un enunciado más restringido en el que sólo exige que el triángulo sea congruente.

Juan Sapiña, en PROBLEMAS GRÁFICOS DE GEOMETRÍA. LITOGRAF. MADRID 1965, propone, con el número 371, un enunciado más restringido en el que sólo exige que el triángulo sea homotético (de lados paralelos).

Resolvamos el problema general.

Resolvamos el problema general:

DADOS TRES CÍRCULOS DE CENTROS O, O’, O” CONSTRUIR UN TRIÁNGULO SEMEJANTE AL TRIÁNGULO OO’O” CUYOS VÉRTICES ESTÉN, RESPECTIVAMENTE, SOBRE LOS TRES CÍRCULOS DADOS

0. INTRODUCCION

Para abordar la resolución del enunciado, imaginemos que para buscar el triángulo pedido, vamos transformando el triángulo de centros por medio de una dilatación (o contracción) hasta que el triángulo transformado y el original estén en las proporciones requeridas.

Después lo vamos girando lentamente en sentido horario (o antihorario) hasta que el primer vértice transformado se ecuentre sobre su círculo.

Acabamos de hacer una homotecia y un giro. La composición de las dos transformaciones anteriores es una semejanza. La semejanza descrita hasta aquí asegura, sólo, la colocación del primer vértice; por lo tanto, nos preguntamos:

¿Cómo aseguramos, también, la colocación del segundo y tercer vértice?

Para poder contestar nos falta un dato:

¿Respecto a que centro de semejanza (homotecia y giro) hay que transformar el triángulo de centros?

1. SEMEJANZA

Vemos por la INTRODUCCIÓN que nos conviene tener a mano la teoría de la SEMEJANZA.

De la obra de Julius Petersen, mencionada en el enunciado, escogemos los resultados más adecuados para el problema que nos ocupa.

figura 1

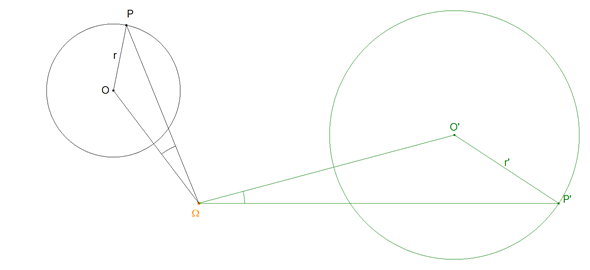
Representamos, en la figura 1, la semejanza de centro Ω que transforma el círculo de centro O y radio r en el círculo de centro O' y radio r'. Considerando P y P' como puntos homólogos, los triángulos OPΩ y O'P'Ω deben ser semejantes, se cumple

Para dos círculos, el centro de rotación está indeterminado, ya que dos cualesquiera de sus puntos pueden ser considerados como punto homólogos; como la razón de las distancias del centro de rotación a los centros de los círculos debe ser la razón de los radios (figura 1), el lugar geométrico del centro de rotación será un círculo^* que corte armónicamente la recta de centros siguiendo la razón mencionada (es el círculo que pasa por los dos centros de homotecia de los dos círculos considerados y que tiene su centro en la recta de centros de esos dos círculos). Si se eligen dos puntos, uno en cada círculo, como puntos homólogos; el centro de rotación queda determinado y se halla de manera muy simple con la ayuda de dos radios homólogos, ya que los centros son siempre puntos homólogos.

* Es el círculo de Apolonio o lugar geométrico de los puntos cuyas distancias a dos puntos fijos están según una razón dada (en este caso r'/r)

1.2 EL CENTRO DE ROTACIÓN DE TRES (3) CÍRCULOS SEMEJANTES (Petersen)

Dados tres sistemas de puntos semejantes O, O' y O"; si un punto Ω es el centro de rotación de O y O' y al mismo tiempo de O' y O", debe ser también el centro de rotación de O y O". Este punto es el centro común de rotación de los tres sistemas.

Si se unen tres puntos homólogos O, O', O" de tres sistemas con centro de rotación en Ω, las razones de las rectas y los ángulos que forman entre ellas son constantes; resulta que la forma del triángulo OO'O" es también constante y, por esta razón, se le llamará el TRIÁNGULO FUNDAMENTAL. Del mismo modo, vemos que a varias figuras semejantes, con un centre común de rotación, corresponde un polígono fundamental de forma constante. Si rota alrededor del centro de rotación de manera que un vértice describe una de las figuras, los otros vértices describirán las otras figuras; cualquier otro punto del plano, considerado como perteneciente al polígono fundamental, trazará una figura semejante a las otras. Como el polígono fundamental llega aa tomar sucesivamente todas sus posiciones, el centro de rotación de las figuras dadas es también el centro de rotación del polígono fundamental en todas sus posiciones.

Hemos dicho que el centro de rotación de dos círculos está indeterminado; pero se puede hallar un centro común de rotación para tres círculos; como este punto está determinado por la intersección de dos círculos, tiene dos soluciones, ambas igualmente admisibles; son los dos puntos cuyas distancias a los centros de los círculos están en la misma proporción que los radios (ver 1.1).

Si tomamos uno de estos puntos de intersección como centro de rotación de los círculos, se puede determinar fácilmente el ángulo de rotación; pues los centros de los círculos son puntos homólogos y las rectas que, desde el centro de rotación, pasan por ellos son rectas homólogas. El triángulo, cuyos vértices son los tres centros, es el triángulo fundamental y cualquier otro triángulo, obtenido uniendo tres puntos homólogos, le es semejante.

Hemos visto que a tres círculos corresponden siempre dos centros comunes de rotación; el triángulo fundamental es el mismo, cualquiera que sea el centro considerado; ya que los tres centros de los círculos son en ambos casos puntos homólogos y se obtiene el triángulo fundamental uniendo tres cualesquiera de estos puntos. Consideremos ahora un punto A sobre uno de los círculos; con homólogos sobre los otros dos en los puntos A'₁ y A"₁, si se emplea uno de los centros de rotación, o bien los puntos A'₂ y A"₂, si nos servimos del otro centro. El triángulo fundamental puede, cuando uno de los vértices cae en A, tomar las dos posiciones AA'₁A"₁ y AA'₂A"₂ y se puede fácilmente demostrar que no puede tomar otras. En efecto, si se resuelve de manera general el problema de colocar el triángulo fundamental de forma que tenga un vértice en A y que los otros dos estén sobre los otros dos círculos, no se obtiene, con las construcciones anteriormente detalladas, más que dos soluciones que deben, en consecuencia, coincidir justo con las que acabamos de hallar del modo anterior.

El triángulo fundamental no puede desplazarse sobre los tres círculos, excepto que sus vértices caigan en puntos homólogos; pero el movimiento puede efectuarse de dos maneras diferentes.

2. APLICACIÓN DE LA TEORÍA A LA SOLUCIÓN

Podemos contestar a las preguntas de la INTRODUCCIÓN siguiendo lo visto en 1.2.

Buscamos el centro común de rotación de los tres círculos; como sus tres centros son puntos homólogos, el triángulo dado es el triángulo fundamental y el centro de rotación encontrado debe ser también el centro de este último triángulo y del buscado. Obtendremos entonces el triángulo buscado transformando el triángulo dado según la semejanza descrita en la INTRODUCCION con centro de rotación en el centro común de los tres círculos.

2.1 EL ENUNCIADO

figura 2

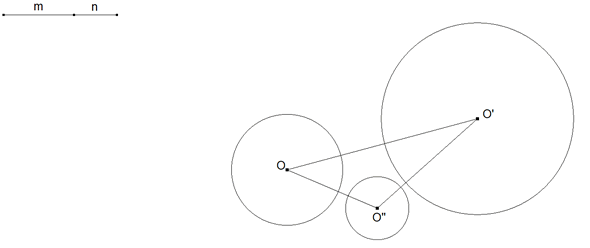
Sea la razón de semejanza ρ y sean los tres círculos con centros en O, O' y O" respectivamente.

2.2 CENTRO COMÚN DE ROTACIÓN DE LOS TRES CÍRCULOS DADOS

figura 3

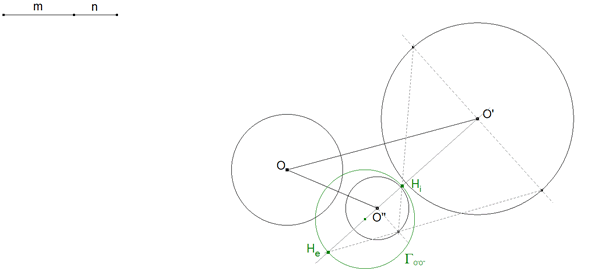
Como decimos en 2.1, el centro de rotación de dos de los círculos (aquí O' y O") se halla sobre el círculo (de Apolonio) que pasa por los dos centros H_i y H_e de las homotecias que transforman un círculo en otro (en este caso O' en O"). Para ello trazamos

-  Recta de centros O'O".

-  Perpendiculares a la recta de centros en O' y O".

-  Rectas que unen los puntos de intersección de perpendiculares y círculos.

-  Las intersecciones de estas rectas con la recta de centros dan H_i y H_e.

-  Con centro en el punto medio de H_i y H_e trazamos por H_i y H_e el círculo Γ_O'O".

-  El centro común de rotación Ω está sobre Γ_O'O"

figura 4

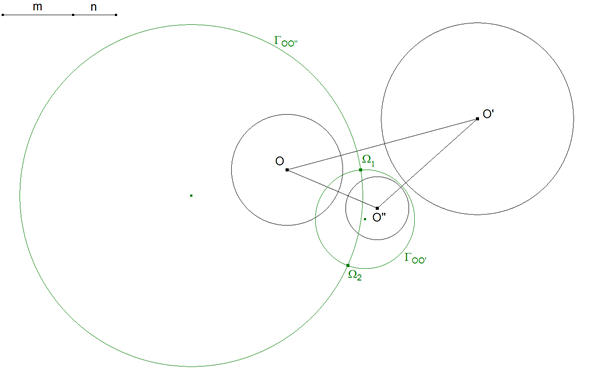
Del mismo modo trazamos Γ_OO' para los círculos O y O'.

Dos círculos se cortan a lo sumo en dos puntos Ω₁ y Ω_2.

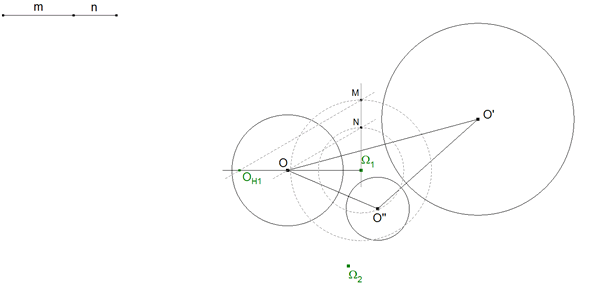
2.3 HOMOTECIA DE RAZÓN m/n

figura 5

Vamos a hallar el transformado de O por una homotecia^* de centro Ω₁ y razón m/n:

-  Recta Ω₁O.

-  Por Ω₁ perpendicular a Ω₁O.

-  Con centro en Ω₁, dos círculos concéntricos de radios m y n.

-  Los círculos cortan respectivamente a la perpendicular en M y N.

-  Recta ON.

-  Por M paralela a ON que corta a Ω₁O en O_H1.

* En lugar de esta construcción podríamos haber usado directamente la herramienta homotecia de CABRI II Plus.

2.4 DETERMINACION DE LA SEMEJANZA

figura 6

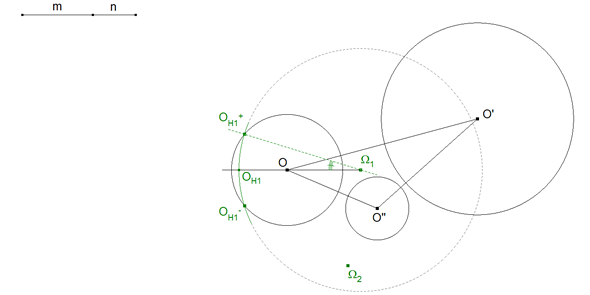
Con centro en Ω₁, rotamos O_H1 hasta encontrar el círculo de centro O_. Obtenemos O_H1⁺, en sentido contrario obtenemos O_H1^-

Como Ω₁O_H1⁺ es la recta homóloga a Ω₁O_H1, podemos obtener el ángulo de rotación en la semejanza como

Hemos determinado la semejanza

2.5 EL GIRO DE CENTRO Ω₁ Y ÁNGULO ∠O_H1Ω₁O_H1⁺

figura 7

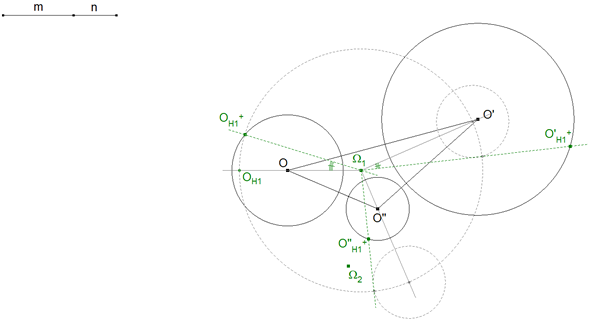
Podemos pues aplicar directamente la rotación^* a las rectas Ω₁O' y Ω₁O", obtenemos las intersecciones con los respectivos círculos en O'_H1⁺ y O"_H1⁺

homólogos respectivos de O' y O".

* En lugar de esta construcción podríamos haber usado directamente la herramienta rotación de CABRI II Plus.

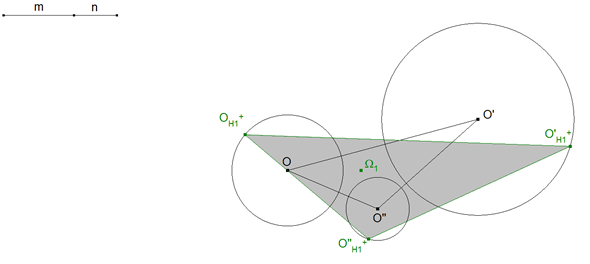
2.6 LA PRIMERA SOLUCIÓN CON CENTRO EN Ω₁

figura 8

Uniendo los vértices O_H1⁺,O'_H1⁺,O"_H1⁺ obtenemos el primer triángulo solución.

El dibujo con todas las líneas auxiliares queda como sigue.

figura 9

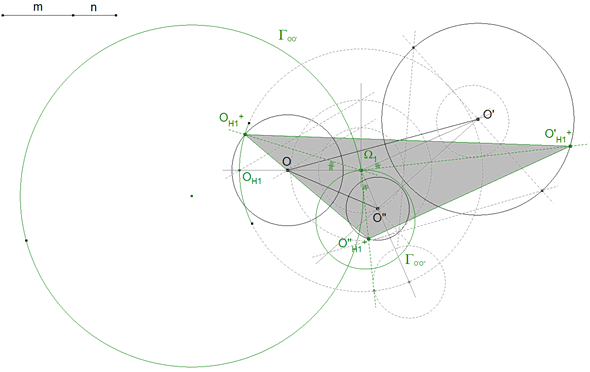
2.7 LA SEGUNDA SOLUCIÓN CON CENTRO EN Ω₁

figura 10

Repetimos la construcción anterior; pero tomando el ángulo contrario.

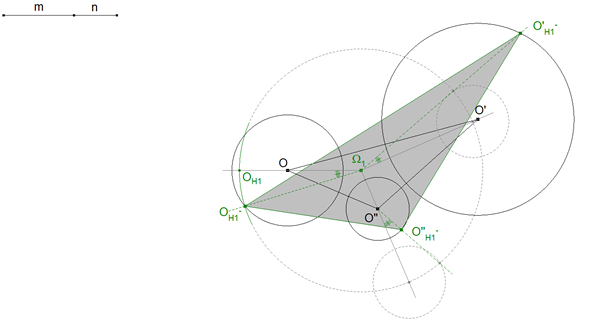
2.8 LA PRIMERA SOLUCIÓN CON CENTRO EN Ω₂

figura 11

primero la homotecia

y luego el giro de O_H2 hasta encontrar el círculo de centro O

obtenemos el ángulo de rotación como

con la semejanza de

y hallamos

homólogos respectivos de O' y O".

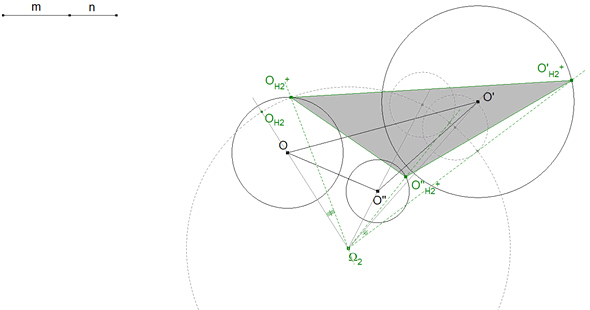
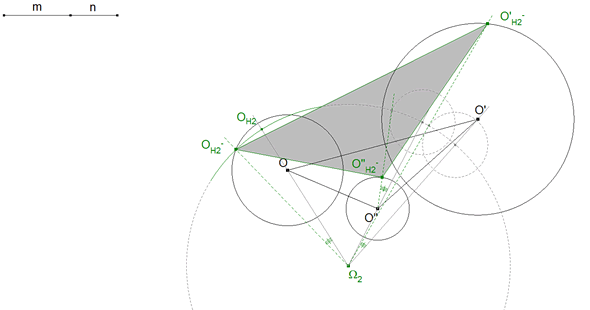
2.9 LA SEGUNDA SOLUCIÓN CON CENTRO EN Ω₂

figura 12

Repetimos la construcción anterior; pero tomando el ángulo contrario.

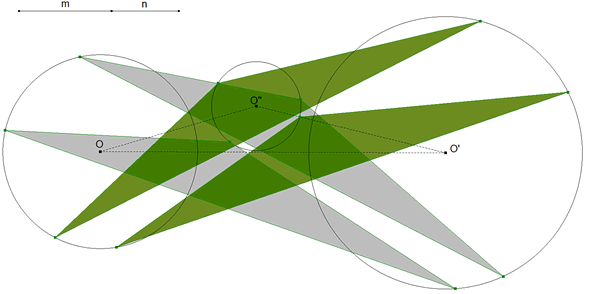
2.10 UN EJEMPLO CON LAS CUATRO SOLUCIONES JUNTAS

figura 13

3. CONCLUSIÓN

Está claro que la existencia de soluciones depende de la razón n/m, de la posición relativa de los círculos y de sus radios.

La consideración anterior, nos define un máximo de 12 soluciones para cada razón n/m.