Problema 287

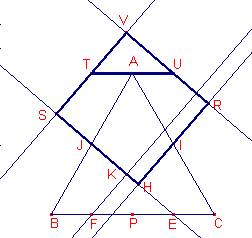
ABC es un triángulo equilátero. I, J y P son los puntos medios de sus lados. Se parte CB en cuatro partes iguales según los puntos E (medio de CP), P y F(medio de PB).

Sea H la proyección ortogonal de I sobre EJ y K la proyección ortogonal de F sobre EJ.

Sea R el simétrico de H en relación al punto I , S el simétrico de K en relación al punto J, U el simétrico de E en relación a I, y T el simétrico de F en relación a J.

Las rectas RU y TS se cortan en V.

UAT, ¿están alineados?

RVSH, ¿es un cuadrado?

Clapponi, P. (1997): Découpage dans un triángulo. Petit X 34,pag 54. [Clapponi es un seudónimo de Philippe Clarou - Bernard Capponi].

Solución de Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València) (17 de diciembre de 2005) (en español):

Sea el lado del triángulo equilátero.

Los triángulos i son semejantes y de proporción 2:1.

. Además són paralelos.

Entonces, T, A U están alineados.

Sea .

Aplicando el teorema de Pitàgores al triángulo rectángulo , .

.

Supongamos que RVSH és un rectángulo, sus ángulos de 90º.

Sea , .

Sea , .

Entonces, els triángulos son semejantes. Aplicando el teorema de Tales:

. Entonces, .

.

Entonces, els triángulos son semejantes. Aplicando el teorema de Tales:

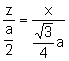, . Entonces, .

.

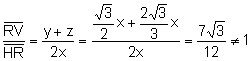Entonces, RVSH no es un cuadrado.