Problema 289 de triánguloscabri

Solución Francisco Javier García Capitán

Figura 1	Figura 2

Análisis

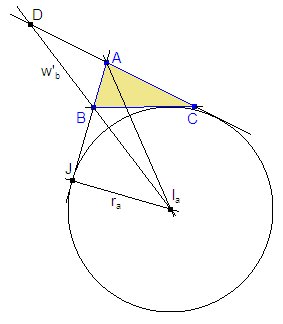
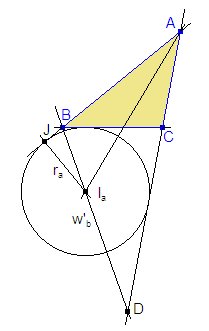
Supongamos el problema resuelto. En las figuras 1 y 2 vemos cómo la bisectriz interior de ángulo A y la bisectriz exterior del ángulo B se cortan en el excentro I_a. También hemos situado los puntos J, proyección ortogonal de I_a sobre AB y D, intersección de la bisectriz exterior de B con la recta AC.

Observamos que en la figura 1 el segmento AI_a es la bisectriz exterior del ángulo A en el triángulo ABD, mientras que en la figura 2 el mismo segmento es la bisectriz interior.

Estas figuras sugieren los siguientes pasos en la solución del problema:

• A partir del ángulo A/2 y de r_a construimos el triángulo rectángulo AJI_a y entonces la longitud AI_a.
• Construcción del triángulo ABD:
  • Siguiendo la figura 1 podemos ahora construir el triángulo ABD, ya que tenemos el ángulo 180-A, el lado opuesto w'_b y la longitud de la bisectriz exterior de dicho ángulo que es AI_a. Recordemos que esta construcción es la tratada en el problema 429 del libro Problemas Gráficos de Geometría, de Juan Sapiña Borja (ver problema 284 del Laboratorio de Triángulos de Ricardo Barroso Campos).
  • Atendiendo a la vez a la figura 2 también podemos construir otro triángulo ABD en el que conocemos el ángulo A, el lado opuesto w'_b y la longitud de la bisectriz interior de dicho ángulo que es AI_a. Para esta construcción podemos adaptar la solución de Juan Sapiña en el problema 284, básicamente intercambiando los papeles de los puntos S y T. En efecto, observemos que si A, a y w_a son conocidos, entonces haciendo una figura parecida a la del problema 284 tendremos que el cuadrilátero ALMS es cíclico y por ello tendrmeos que TL·TA = TM.TS y que TA - TL = w_a.
• Una vez hallado el triángulo ABD, la recta BC la obtenemos haciendo una simetría axial de la recta AB respecto de la recta BD, y el punto C se halla cortando las rectas BC y AD.

La construcción paso a paso

Detallemos los pasos a seguir con Cabri para obtener las dos souciones:

Figura 3. Partimos del ángulo A y los segmentos w'b y ra.

Figura 3

Figura 4. Fijamos un segmento YZ de longitud ra y trazamos el arco capaz de dicho segmento para el ángulo A/2. Por Z levantamos una perpendicular a YZ y obtenemos X en la intersección con el arco capaz. Entonces el segmento XY medirá lo mismo que el segmento AIa de las figuras 1 y 2. Figura 5. Ahora vamos a construir los triángulos ABD. Para ello fijamos un segmento BD de longitud w'b y construimos los arcos capaces BSD y BTD del segmento BD para los ángulos 180º-A y A, respectivamente. Como se ve en la figura, estos dos arcos pertenecen a la misma circunferencia.

Figura 4 Figura 5

Figura 6

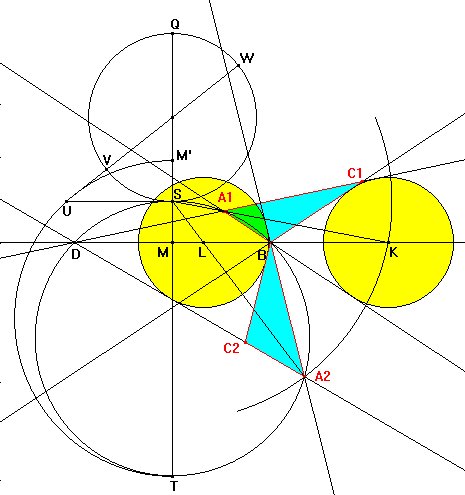
Figura 6. Dibujemos el segmento DB de longitud w'_b. Hallamos el punto simétrico M' de M respecto de S y trazamos una semicircunferencia con diámetro TM'. La perpendicular por S a ST corta a dicha semicircunferencia en U. Tendremos SU^2 = SM'·ST = SM·ST. Ahora, si a continuación del segmento TS trazamos la circunferencia con diámetro SQ = XY = AI_a, y desde U trazamos por su centro una recta que corta a ésta en V y W, tendremos SU^2 = UV·UW, y por tanto que UV·UW=SM·ST. También es UW-WV = VW=SQ=AI_a.

Ahora trazando un arco con centro S y radio UW cortamos en K a la recta DB y la recta SK corta a la circunferencia ST en A₁, siendo A₁K=AI_a la tangente exterior del ángulo A₁ del triángulo A₁DB.

Para obtener la segunda solución hallamos el corte del mismo arco con cetro S y radio UW con la circunferencia de diámetro ST, obteniendo el punto A₂.

Para completar las soluciones en ambos casos repetimos lo dicho anteriormente:

• Una vez hallado el triángulo ABD, la recta BC la obtenemos haciendo una simetría axial de la recta AB respecto de la recta BD, y el punto C se halla cortando las rectas BC y AD.

Discusión

En la segunda solución, si el punto C₂ no cae dentro de la circunferencia de diámetro ST, entonces la solución no es válida ya que el ángulo A₂ no es igual al valor dado del ángulo A, sino su sumplementario.