Problema 289

Propuesto por Luís Lopes (Brasil), es autor de varios libros de matemáticas. Información sobre los mismos puede encontrarse en

http://www.escolademestres.com/qedtexte

Construir un triángulo conociendo A, w'_B (bisectriz exterior del ángulo B) y r_a (radio de la circunferencia ex-inscrita).

Luís Lopes, L. (2005). Comunicación personal

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (17 de diciembre de 2005)

INTRODUCCIÓN

Una manera de atacar este problema es la siguiente,

figura 1

Dado el triángulo solución, supongamos que tenemos el problema solucionado.

figura 2

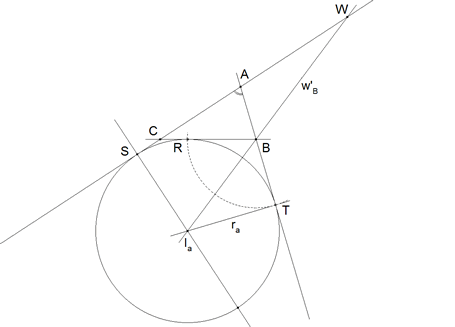
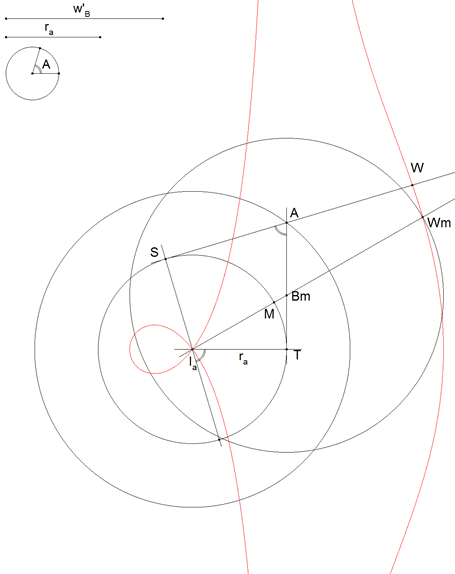
Para ello dibujamos el triángulo ex-inscrito opuesto a A y también la bisectriz externa del vértice B.

Estudiamos la figura y deducimos:

a) El vértice A está sobre dos tangentes a un círculo de radio r_a.

b) Estas dos tangentes forman un ángulo A con puntos de tangencia T y S. El tercer punto de tangencia es R

c )La bisectriz exterior está sobre una recta que pasa por el centro I_a del círculo ex-inscrito.

De a) y b) vemos que hemos de usar el lugar geométrico de los puntos cuyas tangentes a un círculo dado forman un ángulo constante. Este lugar es otro círculo (es multitud la bibliografía que contiene la demostración de esta afirmación).

La segunda idea a usar es trazar una recta variable por I_a que cortará en un punto variable a AT. A partir de ese punto llevamos w'_B y si el punto obtenido cae sobre AS, habremos obtenido la solución.

SOLUCIÓN (en 4 pasos)

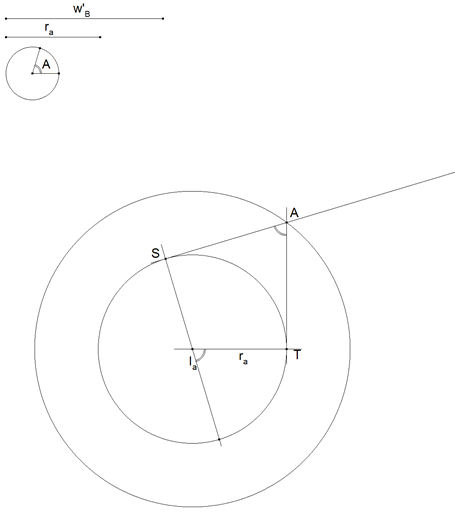
1 EL VÉRTICE A

figura 3

Con centro en I_a, trazamos un círculo de radio r_a (será el círculo ex-inscrito).

Tomamos un punto S cualquiera sobre el círculo y con centro en I_a giramos SI_a un ángulo A. La recta girada corta al círculo en T.

Tomamos el vértice A en la intersección de las tangentes por S y T (podemos colocar A en cualquier punto del círculo donde intersecan las tangentes)

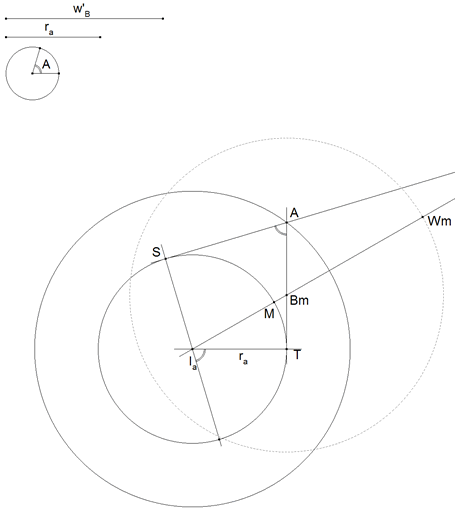
2 EL PUNTO MÓVIL W_m

figura 4

Sobre el círculo ex-inscrito, tomamos un punto móvil M.

La recta I_aM corta a AT en B_m.

Sobre I_aM, a partir de B_m, llevamos la distancia w'_B. Obtenemos W_m.

3 EL PUNTO W

figura 5

A cada punto M corresponde un punto B_m y un punto W_m.

Hallamos el lugar geométrico de W_m cuando M recorre el círculo ex-inscrito. Lugar geométrico harto conocido (Concoide de Nicomedes). Si tomamos a I_a como origen y a I_aT como eje polar, llamando θ al ángulo de M en ese sistema de coordenadas polares. La ecuación es:

Cuando W_m se halle sobre AS tendremos la solución. Por tanto la solución W está en la intersección de la concoide y la recta AS.

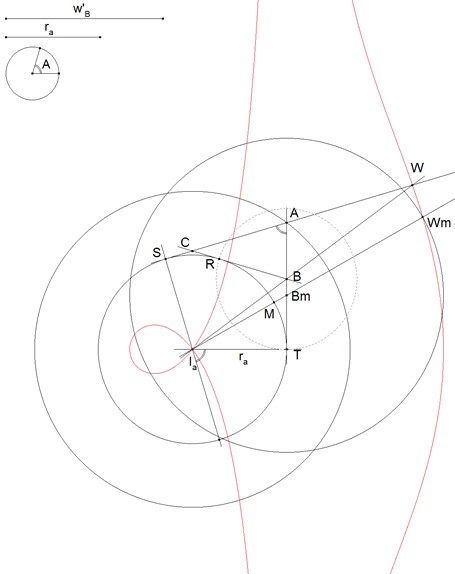
4 LOS VÉRTICES B Y C

figura 6

Trazamos I_aW que corta a AT en B.

Con centro en B y radio BC, círculo que corta, de nuevo, al círculo ex-inscrito en R.

BR corta a AS en C.

5 LA SOLUCIÓN

figura 7