ALGUNAS
PROPIEDADES RELATIVAS A LAS RECTAS DE EULER DE TRES TRIÁNGULOS SIMÉTRICOS
A UN TRIÁNGULO DADO
David Benítez Mojica
Universidad Autónoma de
Coahuila
Nora Lucia Leija
Mendoza
Universidad Autónoma de
Coahuila
Resumen. En este artículo se
demuestran tres propiedades que tienen las rectas de Euler
de los triángulos simétricos a un triángulo dado. Se usó geometría dinámica
para construir la conjetura y se usan propiedades de la geometría analítica
para hacer la demostración.
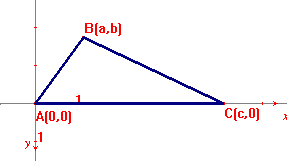
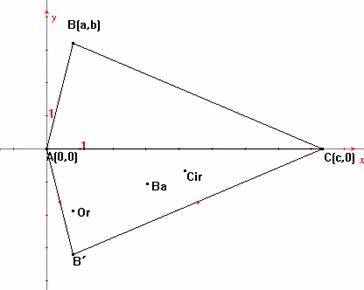
Teorema. Dado un Triangulo ABC , se construyen los triángulos simétricos con respecto a cada un de los lados del triángulo ABC . Las rectas de Euler trazadas en cada uno de estos triángulo se intersectan en un punto P. Además, el punto P y los ortocentros de los triángulos simétricos pertenecen a la circunferencia circunscrita en el triángulo ABC.
|
|
|
|
Figura 1 |
Figura 2 |
Demostración.
- Sin
perdida de generalidad, se puede demostrar el teorema para un triángulo
ABC, con un vértice en el origen de coordenadas y uno de los lados
situados en el eje positivo “x”.
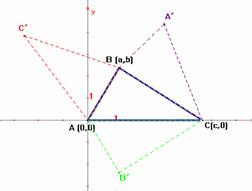
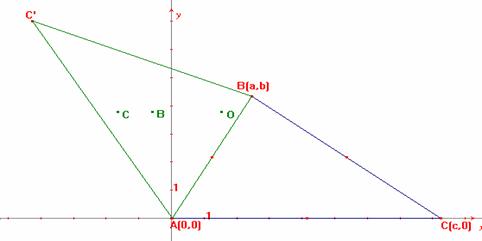
Se construyen los triángulos simétricos en cada uno de los lados (figura
2), donde los puntos son:
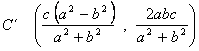
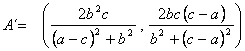
, ![]() ,
,
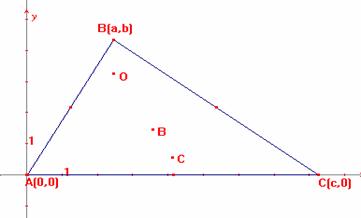
- Enseguida encontraremos los las
coordenadas del ortocentro, baricentro y circuncentro de este triángulo..
Dado
el triángulo ![]() la forma en que se
calculan cada uno de los puntos notables son las siguientes:
la forma en que se
calculan cada uno de los puntos notables son las siguientes:
![]()
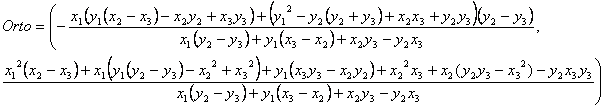
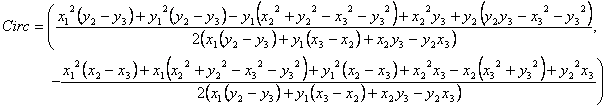
Para el triángulo ABC, donde A = (0,0), B = (a, b), C = (c,0) , se
obtienen:
![]() ,
, ![]() ,
, 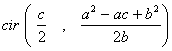
|
|
|
Fig. 3 |
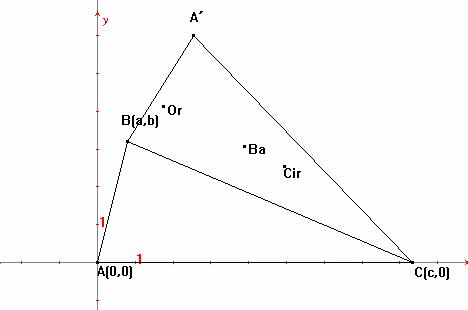
Para el triángulo A’BC, tenemos:
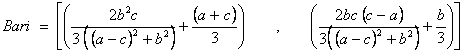
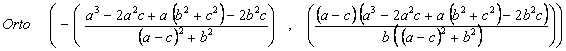

|
|
|
Fig. 4. |
Para el triángulo AB’C se tienen:
![]() ,
, ![]()
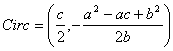
|
|
|
Fig. 5. |
Para el triángulo
ABC’ se tienen:

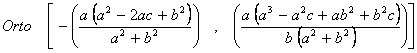
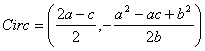
|
|
|
Fig. 6. |
- Utilizando
cada uno de los puntos anteriores, se determinará la ecuación de la recta
de Euler.
Dado los puntos notables ![]() de un triángulo, determinar la ecuación que pasa por estos
puntos:
de un triángulo, determinar la ecuación que pasa por estos
puntos:
![]()
como estas pendientes son iguales porque los
puntos viven en la misma recta, por lo tanto solamente utilizaremos una
pendiente por lo que:
![]()
Tomando solamente el baricentro y ortocentro de los triángulos, se determinaran las rectas de
Euler en cada uno de los triángulos.
La recta de Euler
del triángulo ABC es :
![]()
Ecuación (1)
La
recta de Euler para el triángulo A’BC
es:
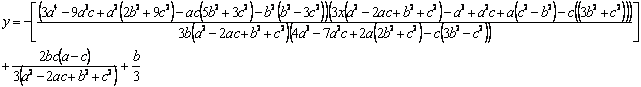 Ecuación (2)
Ecuación (2)
La recta de Euler para el triángulo AB’C es:
![]()
Ecuación (3)
La recta de Euler para el triángulo ABC’ es:
![]()
Ecuación (4)
- Enseguida,
demostraremos si las ecuaciones 2, 3 y 4 se intersectan
en un punto P.
Usando
las ecuaciones 2 y 3 tenemos las coordenadas del punto P
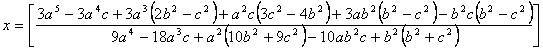
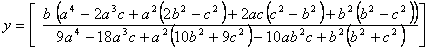
Usando
las ecuaciones 3 y 4 tenemos las coordenadas del punto P
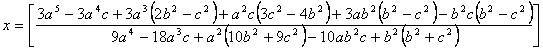
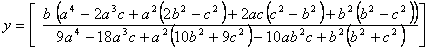
Usando
las ecuaciones 2 y 4 tenemos las coordenadas del punto P
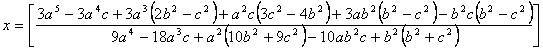
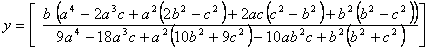
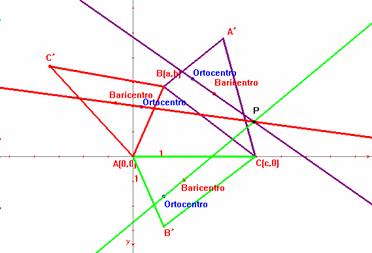
Por
lo anterior podemos determinar que las tres rectas de Euler
formadas son concurrentes en un punto. (P)
|
|
|
Fig. 7 |
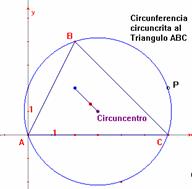
Demostraremos
ahora que el punto P correspondiente a la intersección de las rectas de Euler es un punto de la circunferencia circunscrita al
triangulo ABC.
|
|
|
Fig. 8. |
Siendo
h y k las coordenadas del circuncentro del
triangulo ABC y r la distancia del circuncentro
al punto A de este triangulo, se obtiene la circunferencia:
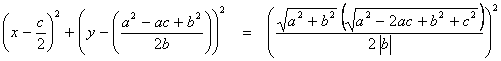
Sustituyendo
las coordenadas ( x , y ) del punto P dentro de la
ecuación anterior y resolviendo para x
e y se obtiene:
![]()
Por
lo que queda demostrado que el Punto P, pertenece a la circunferencia circunscrita al triángulo
ABC
5. Como siguiente paso, demostraremos, que
el punto P, cada uno de los ortocentros de los triángulos simétricos, pertenecen a la
misma circunferencia.
Primero para el
triángulo A’BC, el ortocentro
es:
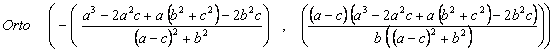
Sustituyendo en:
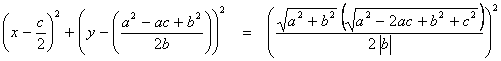
Se
obtiene:
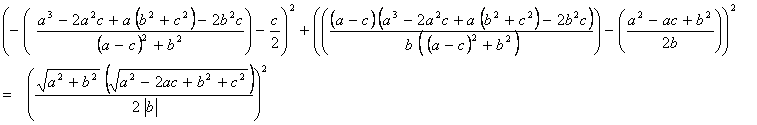
![]()
Por lo que este
punto pertenece a la circunferencia.
![]()
Para el triángulo AB’C, el ortocentro es:
Sustituyendo en:
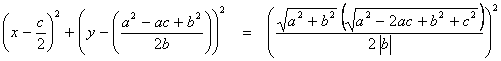
Se obtiene:
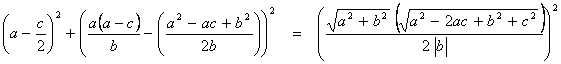
![]()
Por lo que este
punto pertenece a la circunferencia.
Para el triángulo
ABC’, el ortocentro es:
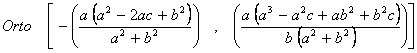
Sustituyendo en:
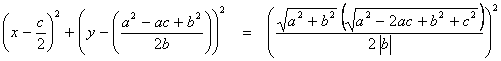
Se obtiene:

Por
lo que los ortocentros pertenecen a la circunferencia circunscrita al Triángulo
ABC.
Por lo tanto, dado el
Triángulo ABC, se construyen los triángulos simétricos en cada un de los lados
(figura 2), las rectas de Euler trazadas en cada uno
de estos triángulo se intersectan en un punto P
(figura 6). Además, los ortocentros de los triángulos
simétricos viven en la circunferencia circunscrita en el triángulo ABC.