Propuesto por David Benítez Mojica y Nora Lucia Leija Mendoza, profesores de la Universidad Autónoma de Coahuila (Méjico)

Problema 290.- Dado un triangulo ABC, se construyen los triángulos simétricos con respecto a cada uno de los lados del triángulo ABC . Las rectas de Euler trazadas en cada uno de estos triángulo se intersectan en un punto P. Además, el punto P y los ortocentros de los triángulos simétricos pertenecen a la circunferencia circunscrita en el triángulo ABC.

Benitez, D, Leija, N.L. (2005): Comunicación personal.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León de Salamanca.

Que los ortocentros de los triángulos simétricos del ABC están en la circunferencia circunscrita es inmediato. En el problema nº 166 demostramos que los simétricos de los ortocentros respecto de los pies de cada altura están en esta circunferencia.

Hay otra propiedad que nos interesa para la resolución del problema.

Si llamamos H_a a la proyección del ortocentro H desde A sobre la c. circunscrita se verifica que el ángulo H_aBH_c es el doble del ángulo CBA. Basta observar en la figura adjunta cómo el ángulo en B es la suma de los ángulos etiquetados como 1 y 2: tienen como suplementario el mismo ángulo H_aHH_c.

En el triángulo AHC, áng(1) + áng(2)=180 – áng AHC.

En el cuadrilátero MHNB, áng B + áng H_aHH_c = 180.

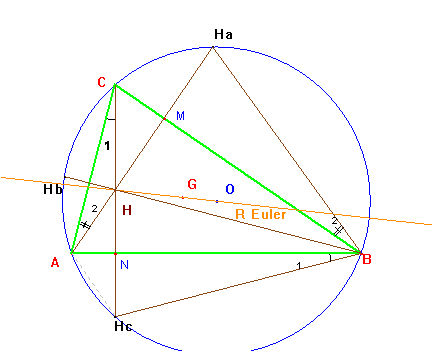
En consecuencia, el arco capaz del segmento H_aH_c y amplitud el doble del ángulo ABC es el arco H_aBH_c de la circunferencia circunscrita.

Vamos a demostrar que las rectas de Euler de los triángulos A’BC y AC’B se cortan en un punto P de la circunferencia circunscrita.

Es evidente que estas rectas, r_a, r_c pasan por los puntos H_a y H_c respectivamente.

Podemos suponer que de la recta r_a se pasa a la r_c componiendo una simetría respecto al lado a=BC (que nos lleva a la recta de Euler de ABC) con otra simetría respecto al lado c=AB. El resultado de la composición de dos simetrías axiales es un giro de centro el punto B de intersección de los ejes y ángulo el doble del formado por ellos. Así pues, las rectas r_a, r_c que pasan por los puntos H_a y H_c, forman un ángulo igual a dos veces el ángulo de las rectas a y b. Su punto de intersección estará situado en el arco capaz del segmento H_aH_c y amplitud el doble del ángulo ABC, por tanto, un punto P de la circunferencia circunscrita.

Una recta queda fija dando dos puntos, si r_a, ha de cortar a r_b en la c. circunscrita, este punto es necesariamente P, ya que r_b no pasa por H_a. Y con esto se concluye.