Usemos
el método de observar la figura y detectar en en ella alguna parte que
pueda construirse con los datos del problema. Con esa parte construida, hallamos
el triángulo buscado.|
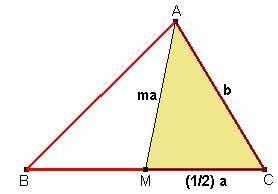
15. Construir un triángulo dados dos lados y la mediana relativa a uno de ellos. |
|
Ruiz, A. (1926): Nociones y ejercicios de aritmética y geometría. (pag 235) |
Solución de Francisco Javier García Capitán
Podemos suponer, sin pérdida de generalidad, que conocemos a, b, y ma.
Usemos
el método de observar la figura y detectar en en ella alguna parte que
pueda construirse con los datos del problema. Con esa parte construida, hallamos
el triángulo buscado.
En este caso, las dos partes del proceso son sencillas, ya que podemos construir fácilmente la mitad derecha del triángulo buscado, el triángulo AMC.
Y una vez hecho esto, hallaremos B como el simétrico de C respecto de M.