Problema 291

15. Construir un triangle coneguts dos costats i la mitjana corresponent a un d’ells.

Ruiz, A. (1926): Nociones y ejercicios de aritmética y geometría. (pag 235)

Solució de Ricard Peiró:

Coneguts

Figura barroso291.fig

Applet created on 16/01/06 by Ricard Peiró i Estruch with CabriJava

Passos de construcció amb regle i compàs:

a) Dibuixar el segment .

b) Dibuixar el punt mig D del segment .

c) Dibuixar la circumferència de centre C i radi b

d) Dibuixar la circumferència de centre D i radi .

e) El vèrtex A és la intersecció de les circumferències , .

f) Calcular les mesures del costat c i dels angles.

Nota: Una vegada resolt el problema podem notar que el problema té solució

si i només si el triangle es pot construir, és a dir,

si s’acompleixen les tres igualtats triangulars:

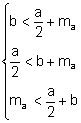
Determinació analítica.

Mètode 1:

La mitjana d’un triangle en funció dels costats és:

Resolent l’equació en la incògnita c, determinarem el costat .

Aplicant el teorema del cosinus al triangle calculem els angles:

Mètode 2:

Aplicant el teorema del cosinus al triangle calculem els angles C i :

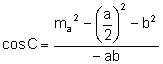
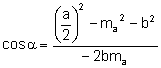
Aleshores,

Aplicant el teorema del cosinus al triangle :
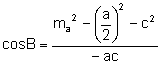