Problema 291

15. Construir un triángulo dados dos lados y la mediana relativa a uno de ellos.

Ruiz, A. (1926): Nociones y ejercicios de aritmética y geometría. (pag 235)

Solución de Ricard Peiró:

Conocidos

Figura barroso291.fig

Applet created on 16/01/06 by Ricard Peiró i Estruch with CabriJava

Pasos de construcción con regla y compás:

a) Dibujar el segmento .

b) Dibujar el punto medio D del segmento .

c) Dibujar la circunferencia de centro C y radio b

d) Dibujar la circunferencia de centro D y radio .

e) El vértice A es la intersección de las circunferencias , .

f) Calcular las medidas del lado c y de los ángulos.

Nota: Una vez resuelto el problema podemos notar que el problema tiene solución si y solo si el triángulo se puede construir, es decir, si se cumplen las tres desigualdades triangulares:

.

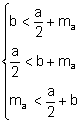Determinación analítica.

Método 1:

La mediana de un triángulo en función de los lados es:

Resolviendo la ecuación en la incógnita c, determinaremos el lado .

Aplicando el teorema del coseno al triángulo calculamos los ángulos:

.

Método 2:

Aplicando el teorema del coseno al triángulo calculamos los ángulos C y :

.

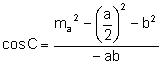
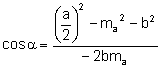Entonces,

Aplicando el teorema del coseno al triángulo :

.

.

.
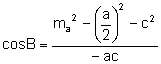