Problema 292

Demostreu que la condició necessària i suficient q fi que l’altura , la mitjana i una de les bisectrius de l’angle C d’un triangle siguen concurrents és que:

.

Thébault, V. (1949): Mathematics Magazine. Vol. 23, No. 2, Nov. - Dec., 1949, p. 103

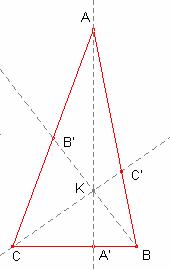Solució:

a) Suposem que B és un angle agut.

Aplicant el teorema de Ceva, , , (bisectriu interior) són 3 cevianes. Les cevianes s’intersecten si i només si .

Aplicant la propietat de la bisectriu:

Per ser B’ punt mig del costat , .

Aplicant raons trigonomètriques al triangle rectangle :

, , (bisectriu interior) s’intersecten si i només si

.

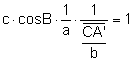Aplicant el teorema dels sinus i tenint en compte que .

, , (bisectriu interior) s’intersecten si i només si ,

si i només si, .

b) Suposem que B és obtús

Siga (bisectriu exterior) C’ en la prolongació del costat

, , s’intersecten si i només si . (veure nota final)

Aplicant la propietat de la bisectriu:

Per ser B’ punt mig del costat , .

Aplicant raons trigonomètriques al triangle rectangle :

.

, , (bisectriu exterior) s’intersecten si i només si

.

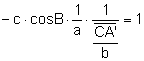Aplicant el teorema dels sinus i tenint en compte que .

, , (bisectriu exterior) s’intersecten si i només si ,

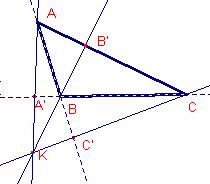si i només si, .

Nota:

(exterior al triangle) A’ en la recta BC,

(interior al triangle) B’ en ,

(exterior al triangle) C’ en la recta AB

, , s’intersecten si i només si .

Demostració:

Suposem que les rectes AA’, BB’, CC’ es tallen en un punt K.

Dos triangle que tenen la mateixa altura les àrees són proporcionals a les bases.

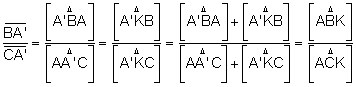
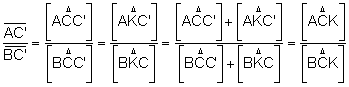
Multiplicant les tres igualtats:

Siguen els punts A’ de la recta BC, C’ de la recta AB tal que:

(1)

Siga K el punt intersecció de .

Siga la recta r que passa pels punt B, K que talla el costat en D

Vegem que D es igual a B’

i es tallen en K aleshores, (2)

Igualant les dues (1), (2) expressions,

Els punts D, B’ pertanyen al costat i divideixen el costat amb la mateixa raó, per tant D i B’ coincideixen.

Per tant, , , s’intersecten.