Problema 294

Donat un triangle i tres punts A’, B’, C’ sobre els costats , respectivament, les circumferències circumscrites als triangles , , concorren en un punt M que s’anomena punt Miquel (August Miquel, 1883, matemàtic francés)

Solució Ricard Peiró:

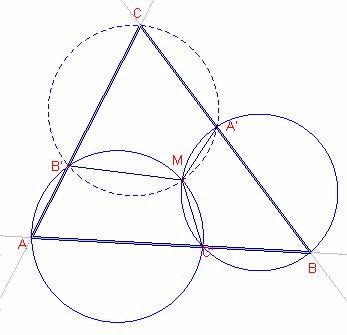
Siga M la intersecció de les circumferències circumscrites als triangles , .

El quadrilàter AC’MB’ és cíclic, pel teorema de Tolomeu, els angles oposats del quadrilàter són suplementaris, aleshores,

El quadrilàter BA’MC’ és cíclic, pel teorema de Tolomeu, els angles oposats del quadrilàter són suplementaris, aleshores,

Els angles i l’angle del quadrilàter CB’MA’ són suplementaris, aplicant el teorema de Tolomeu, el quadrilàter CB’MA’ és cíclic, per tant M pertany a la circumferència circumscrita al triangle .

Nota: Si els punts A’, B’, C’ pertanyen a la prolongació dels costats el teorema de Miquel també s’acompliria i la demostració seria anàloga.

Prova amb Cabri:

Figura barroso294.fig

Applet created on 1/02/06 by Ricard Peiró with CabriJava