Problema 294

For a triángulo ABC and three points A', B', and C', one on each of its sides, the three Miquel circles are the circles passing through each polygon vertex and its neighboring side points (i.e., AC'B', BA'C', and CB'A'). According to Miquel's theorem, the Miquel circles are concurrent in a point M known as the Miquel point

.Para un triángulo ABC y tres puntos A', B', y C', uno en cada uno de sus lados , las tres circunferencias de Miquel son las que pasan por cada vértice y los puntos sobre los lados correspondientes ( es decir, por AC'B', BA'C', y C B'A'). De acuerdo con el teorema de Miquel, las circunferencias de Miquel son concurrentes en un punto M conocido como punto de Miquel.

Eric W. Weisstein. "Miquel Triángulo." From MathWorld--A Wolfram Web Resource.

http://mathworld.wolfram.com/MiquelsTheorem.html

Solución Ricard Peiró:

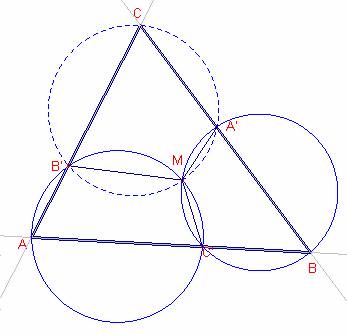
Sea M la intersección de las circunferencias circunscritas a los triángulos , .

El cuadrilátero AC’MB’ es cíclico, por el teorema de Tolomeo, los ángulos opuestos del cuadrilátero son suplementarios, entonces,

El cuadrilátero BA’MC’ es cíclico, por el teorema de Tolomeo, los ángulos opuestos del cuadrilátero son suplementarios, entonces,

Los ángulos y el ángulo del cuadrilátero CB’MA’ son suplementarios, aplicando el teorema de Tolomeo, el cuadrilátero CB’MA’ es cíclico, por tanto M pertenece a la circunferencia circunscrita al triángulo .

Nota: Si los puntos A’, B’, C’ pertenecen a la prolongación de los lados el teorema de Miquel también se cumple y la demostración es análoga.

Prueba con Cabri:

Figura barroso294.fig

Applet created on 1/02/06 by Ricard Peiró with CabriJava