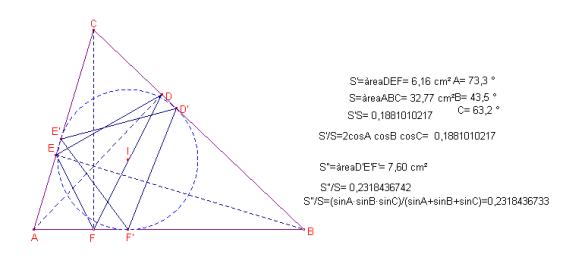
Problema 296

Siga el triangle un triangle de costats . Siga un triangle inscrit en , tal que els punts D, E, F, estan respectivament sobre els costats .

Siga S’ l’àrea de i S l’àrea del triangle , es demana:

a) Determineu el quocient de les àrees .

b) Quant val si les cevianes , concorren?.

c) Si D, E, F són els peus de les mitjanes .

d) Si D, E, F són els peus de les bisectrius interiors .

e) Si D, E, F són els peus de les altures

f) Si D, E, F són els peus de les perpendiculars sobre els costats des de l’incentre

.

g) Compareu els resultats de e) i f).

Scheffer, J.( 1881 ) : "On the Ratio of the Area of a Given Triangle to That of an Inscribed Triangle" The Analyst, (Nov.) Vol.8 N.6 , pp.173-174

Solució de Ricard Peiró:

Siga , aleshores, , .

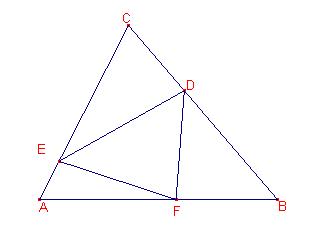
, aleshores, , .

, aleshores, , .

a)

Dos triangles que tenen la mateixa altura les àrees són proporcionals a les bases:

, Multiplicant les dues expressions:

.

Anàlogament:

(1)

b)

Les tres cevianes concorren si i només si

Substituint en l’expressió (1)

c)

Les tres mitjanes s’intersecten en un punt.

D, E, F són els punts mig dels costats, aleshores, .

Aplicant la relació de l’apartat b):

.

d)

Les tres bisectrius s’intersecten en un punt.

Aplicant la propietat de la bisectriu

, aleshores,

, aleshores,

Aplicant la relació de l’apartat b):

.

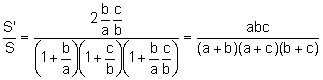d)

Les tres altures s’intersecten en un punt.

Aplicant el teorema de Pitàgores al triangle rectangle :

Aplicant el teorema de Pitàgores al triangle rectangle :

Igualant les expressions:

.

Resolent l’equació en s:

Anàlogament:

Aplicant la relació de l’apartat b):

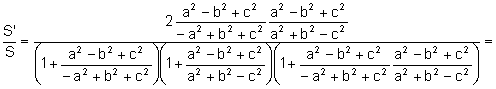
Aplicant el teorema del cosinus al triangle

.

f)

Siguen D, E, F els punts de tangència de la circumferència inscrita i els costats:

Les cevianes , concorren.

.

.

.

.

Aplicant la relació de l’apartat b):

.

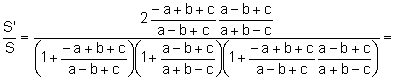
Aplicant la fórmula d’Heró i la fórmula trigonomètrica de l’àrea:

Aleshores,

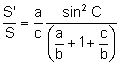. Aplicant el teorema dels sinus al triangle :

.

.

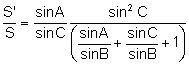g) Compareu els resultats de e) i f).

, .

.