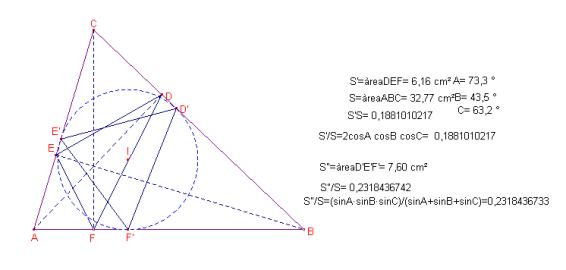
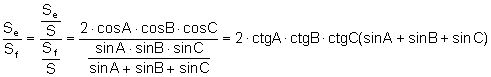Problema 296

Siga el triángulo un triángulo de lados . Siga un triángulo inscrito en , tal que los puntos D, E, F, están respectivamente sobre los lados .

Siga S’ el área de y S el área del triángulo , se pide:

a) Determina el cociente de las áreas .

b) ¿Cuánto vale si las cevianas , concurren?.

c) Si D, E, F son los pies de las medianas .

d) Si D, E, F son los pies de las bisectrices interiores .

e) Si D, E, F son los pies de las alturas

f) Si D, E, F son los pies de les perpendiculares sobre los lados desde el incentro

.

g) Comparar los resultados de e) y f).

Scheffer, J.( 1881 ) : "On the Ratio of the Area of a Given Triángulo to That of an Inscribed Triángulo" The Analyst, (Nov.) Vol.8 N.6 , pp.173-174

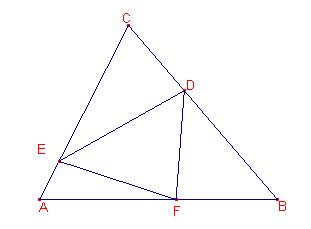
Solución de Ricard Peiró:

Sea , entonces, , .

, entonces, , .

, entonces, , .

a)

Dos triángulo que tienen la misma altura las áreas son proporcionales a las bases:

, Multiplicando las dos expresiones:

.

Análogamente:

(1)

b)

Las tres cevianas concurren si y sólo si

Substituyendo en la expresión (1)

c)

Las tres medianas se intersectan en un punto.

D, E, F son los puntos medios de los lados, entonces, .

Aplicando la relación del apartado b):

.

d)

Las tres bisectrices se intersectan en un punto.

Aplicando la propiedad de la bisectriz

, entonces,

, entonces,

Aplicando la relación del apartado b):

.

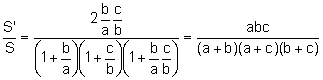d)

Las tres alturas se intersectan en un punto.

Aplicando el teorema de Pitágoras al triángulo rectángulo :

Aplicando el teorema de Pitágoras al triángulo rectángulo :

Igualando les expresiones:

.

Resolviendo la ecuación en s:

Análogamente:

Aplicando la relación del apartado b):

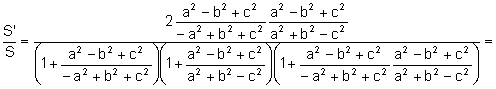
Aplicando el teorema del coseno al triángulo

.

f)

Sean D, E, F los puntos de tangencia de la circunferencia inscrita y los lados:

Las cevianas , concurren.

.

.

.

.

Aplicando la relación del apartado b):

.

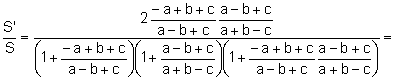
Aplicando la fórmula de Herón y la fórmula trigonométrica del área:

Entonces,

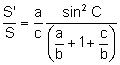. Aplicando el teorema de los senos al triángulo :

.

.

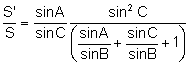g) Comparar los resultados de e) i f).

, .