Problema
298
Construïu
un triangle equilàter 
i una circumferència (C) de centre C que passa
per B.
a) La
circumferència (C) passa per A?. Per què?
Construïu
la tangent a la circumferència (C) pel punt A. Talla la recta BC en el punt P.
Construïu
la tangent a la circumferència (C). Siga S un punt qualsevol d’aquesta tangent.
b) Què
pots dir del triangle 
? Justifica-ho amb molta cura.
Clapponi, P. (1997): Activité…
deux tangentes.. Petit X 44, pag. 50. [Clapponi es un seudónimo de Philippe
Clarou - Bernard Capponi].
Solució
de Ricard Peiró:
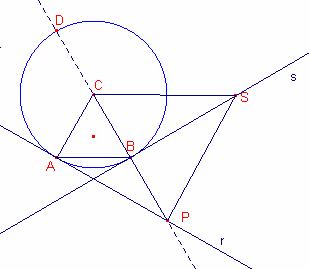a)
Per
ser el triangle equilàter 
aleshores, la
circumferència de centre C que passa per B també passa per A.
b)
Siga
la recta r tangent a la circumferència en el punt A.
La
recta r és perpendicular al radi 
.
Siga
P la intersecció de la recta r i la prolongació del costat 
.
L’angle
és exterior a la
circumferència per tant la seua mesura és la semidiferència dels arcs que
abraça.
La
recta BC talla la circumferència en el punt D.
és un diàmetre.
per ser el triangle
rectangle.
.
Aleshores,
.
El
triangle 
és rectangle, 
. A més a més 
.
Aleshores,
.
Com
que , tenim que 
.
Siga
la recta s tangent a la circumferència en el punt B.
La
recta s és perpendicular a 
, a més a més B és el punt mig de 
.
Aleshores,
la recta s és mediatriu del segment .
Siga
S un punt de la recta s, 
per pertànyer a la
mediatriu. Aleshores el triangle és isòsceles.